1
Plot[{{A0 E^(-k1 t), -((
     A0 E^(-k1 t - k2 t) (-E^(k1 t) + E^(k2 t)) k1)/(k1 - k2)), (
    A0 E^(-k1 t - 
      k2 t) (-E^(k1 t) k1 + E^(k1 t + k2 t) k1 + E^(k2 t) k2 - 
       E^(k1 t + k2 t) k2))/(k1 - k2)} /. {A0 -> 1, k1 -> 4, 
    k2 -> 10}}, {t, 2, 0}]

How may I color each curve differently?

xslittlegrass
  • 27,549
  • 9
  • 97
  • 186
ErikSaiyan
  • 11
  • 1
  • Plot[Evaluate[{A0 E^(-k1 t), -((A0 E^(-k1 t-k2 t) (-E^(k1 t)+E^(k2 t)) k1)/(k1-k2)), (A0 E^(-k1 t-k2 t) (-E^(k1 t) k1+E^(k1 t+k2 t) k1+E^(k2 t) k2-E^(k1 t+k2 t) k2))/(k1-k2)} /. {A0->1, k1->4, k2->10}], {t, 2, 0}] – Bill May 06 '16 at 06:09
  • 3
    Or Plot[...,Evaluated->True]. – xslittlegrass May 06 '16 at 06:11

1 Answers1

0

For a verry nice Q & A see Using Evaluate and Evaluated -> True in Plot 

Plot[{{A0 E^(-k1 t)
, -((A0 E^(-k1 t - k2 t) (-E^(k1 t) + E^(k2 t)) k1)/(k1 - k2))
, (A0 E^(-k1 t - k2 t) (-E^(k1 t) k1 + E^(k1 t + k2 t) k1 + E^(k2 t) 
k2 - E^(k1 t + k2 t) k2))/(k1 -k2)} /. {A0 -> 1, k1 -> 4, k2 -> 10}}
, {t, 2, 0}
, Evaluated -> True]

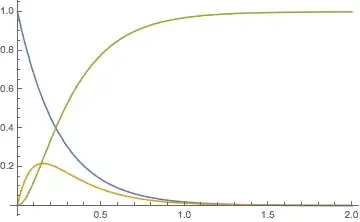
enter image description here

Plot[{{A0 E^(-k1 t)
, -((A0 E^(-k1 t - k2 t) (-E^(k1 t) + E^(k2 t)) k1)/(k1 - k2))
, (A0 E^(-k1 t - k2 t) (-E^(k1 t) k1 + E^(k1 t + k2 t) k1 + E^(k2 t) 
k2 - E^(k1 t + k2 t) k2))/(k1 -k2)} /. {A0 -> 1, k1 -> 4, k2 -> 10}}
, {t, 2, 0}
, Evaluated -> True
, PlotStyle -> {Red, Green, Blue}]

enter image description here

And contemplate the following:

A0 = 1; k1 = 4; k2 = 10;

Plot[{{A0 E^(-k1 t)
, -((A0 E^(-k1 t - k2 t) (-E^(k1 t) + E^(k2 t)) k1)/(k1 - k2))
, (A0 E^(-k1 t - k2 t) (-E^(k1 t) k1 + E^(k1 t + k2 t) k1 + E^(k2 t) 
k2 - E^(k1 t + k2 t) k2))/(k1 -k2)}}
, {t, 2, 0}]
Community
  • 1