Solution for Imaginary part of equation

Question

I have a function Il12i[-0.001, -0.001, w, 0, 1, 0, 0.1002] which is depends on 1 variable w and it is real if w > -3666 (this number I found from graphs). This function is very complicated numerical function as result of numeric integration, some algebraic system solution and NDSolve. I cannot put it here, because it takes something like 10 pages of text.

I need to solve something like this Abs[ Im[ Il12i[-0.001, -0.001, w, 0, 1, 0, 0.1002] ]] > 0

In other words I need to find point, where this function becomes complex.

NSolve does not work at all, as I understand from documentation for complicated function it is better to use FindRoot.

I tried something like this

FindRoot[Abs[Im[Il12i[-0.001, -0.001, w, 0, 1, 0, 0.1002]]] == 0.001, {w, -3700.0}]

but it gives me wrong result {w -> -3639.24} and error message "Encountered a singular Jacobian at the point {w} = {-3639.24}. Try \ perturbing the initial point(s). "

I found a little bit similar problem here HarmonicNumber problem and I understand that I can try to play with WorkingPrecision like this

FindRoot[Abs[Im[Il12i[-0.001, -0.001, w, 0, 1, 0, 0.1002]]] == 0.001, {w, -3700.0}, AccuracyGoal -> Infinity, PrecisionGoal -> 5, WorkingPrecision -> 10000]

but it did not helped.

I made a plot to understand how Im and Re of this function looks like and it it below

and I know that this equation has only one solution, I even know where it is approximately from graph (w=-3666), but I cannot find it :(.

My final goal to find many solutions of similar equations to find how this point where function becomes complex depends on parameters a, b, c like this Il12i[a, b, w, 0, 1, 0, c], this is why I cannot use solution from graph or I will need to make hundreds graphs with different parameters a, b, c.

UPDATE:

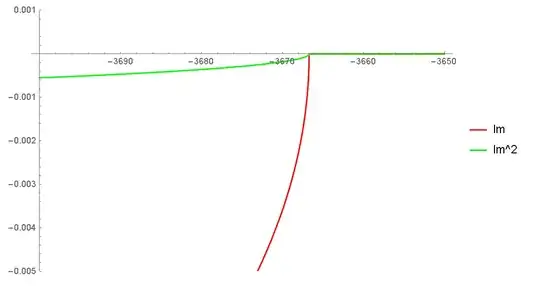
If I try to use this function in ^2, it is still complex and it is very similar and returns the same error. Here is the graph of normal function and ^2.

I prepared some numerical test data from this function and upload it here https://drive.google.com/open?id=0B8TaBGM8Qgp5ZHROUlRscjVKbVk

It can be loaded and returns the same error by this code

Get["C:\\data\\temp\\ccc\\1.zzz"]

Plot[{Im[IIINf[w]]}, {w, -3700, -3650}, PlotLegends -> {"Im"}, 
 PlotStyle -> {Red}]

FindRoot[Abs[Im[IIINf[w]]] == 0.001, {w, -3700}, 
 WorkingPrecision -> 1000]

Since the imaginary part of an expression is real, instead of Abs[expr] > 0 try Sqrt[expr^2] > 0. The derivatives will then exist and Mathematica may do better. — Bob Hanlon, May 07 '16 at 23:05
Given the character of the curves in the plot, try solving Il12i[w]^2 == 0 with FindRoot.. — bbgodfrey, May 08 '16 at 02:58
Looking at the graph I would surmise Newton's method will shoot from -3700 to a part where Im[...] is zero, hence that singular Jacobian. You might try constraining it, maybe use FindMinimum[{(Im[expr]-.001)^2,x<=-3667},{w,-3700}] and see if that avoids the trouble zone. — Daniel Lichtblau, May 08 '16 at 15:04
Thanks a lot to everyone for answers. But Unfortunately it did not help. This function in power 2 is still complex and graphs looks almost the same like shown in my update. FindMinimum returns almost the same value as I put here x<=-3667. I am going to upload some data as file, where it is possible to reproduce the issue. — Zlelik, May 08 '16 at 21:26
Looks like I found solution. I made Numerical Differentiation with ND[] function and because derivative has some singularity at this point in numerical approach it comes like a maximum and later FindMaximum[] function did the task. I will try to post code later today. — Zlelik, May 09 '16 at 14:42
@Zlelik Rather than posting your solution as part of you question, please post it as a self-answer. These are encouraged on Stack Exchange, and it will cause your question to show up answered to future searches. — MarcoB, May 10 '16 at 16:13

score 0 · Accepted Answer · answered May 17 '16 at 21:34

I found a solution by myself. If I continue my uploaded example, where I dump function values to the file and load it later, it will be like this.

Calculate Numerical derivative from source function

Needs["NumericalCalculus`"]

IIIDNf[x_] = ND[IIINf[w], w, x]
Just to see how it looks like I plot the graph of derivative (green) and source function (red).

Find maximum for derivative of my function

FindMaximum[Im[IIIDNf[w]], {w, -3700}]

I check it with many parameters and it works very good if I put start point on the left side of the maximum.

my real example with some more tuning for better precision.

FindMaximum[ Im[DNIl12i[-0.001, -0.001, w]], {w, -1200000}, AccuracyGoal -> Infinity, PrecisionGoal -> 5, WorkingPrecision -> 50]

I am open for comments. I think it can be used to find solution of some equations with sharp (not smooth) functions. Because calculation of numeric derivative makes function more smooth.

Solution for Imaginary part of equation

1 Answers1