2

My Hamiltonian is 

HI(t) = 
  Piecewise[
    {{H1, n τ <= t <= (n + 1/2) τ}, 
     {H2, (n + 1/2) τ <= t <= (n + 1) τ}}]

enter image description here where

  H1 = {{x, y, 0}, {y, x, 0}, {0, 0, x}}; 
  H2 = {{x, y, z}, {y, x, 0}, {z, 0, x}};

Lets take values for numerical solution: 

x = 2; y = 3; z = 4; z = 4;

and

n = 20; τ = 0.5;

initial condition:

{0,1,0};

I want to solve the time-dependent Schrödinger equation for the piecewise periodic Hamiltonian:

$$i\frac{\partial\psi(t)}{\partial t}=HI(t)\psi(t)$$

We can also think this problem as

$$i \psi'(t) - HI(t) \psi(t) = 0,$$

where $HI(t)$ is piecewise continuous function.

santosh
  • 603
  • 3
  • 11
  • Your Hamiltonian isn't hermitian, so it violates probability conservation. Also, you need to specify an initial condition. Then use NDSolve. – Jens May 08 '16 at 02:10
  • Hi Jens, It is not a duplicate question, here I need to deal with Piecewise periodic Hamiltonian which is not state forward. I did not write the Hamiltonian correct previously. Please look at this again, I also define the initial condition as well... – santosh May 08 '16 at 03:13
  • OK, I posted an answer addressing in particular the Piecewise issue. This does indeed look like a separate issue, and since the Hamiltonian is now fixed it's worth keeping as a question in its own right, I think. – Jens May 08 '16 at 04:21

2 Answers2

2

I think possible issue here was the fact that Piecewise is used here to distinguish between different matrices inside NDSolve. Since Piecewise remains unevaluated until you put in specific time values, this hides the matrix structure from NDSolve at the initial step where it parses the differential equation.

Also, I think the periodicity you want to achieve is formulated in a way that can't be used in an actual computation, so I would suggest rewriting it with Mod instead.

To be on the safe side, I used MapThread to put the Piecewise inside the matrices (acting element-wise). Then I also defined the solution vector element-wise and used Thread in the vectorial differential equation to convert it into a system of equations. Here is the result:

H1 = {{x, y, 0}, {y, x, 0}, {0, 0, x}}; H2 = {{x, y, z}, {y, x, 
   0}, {z, 0, x}};

x = 2; y = 3; z = 4; z = 4; n = 20; τ = 0.5;

h[t_] = MapThread[
  Piecewise[{{#1, Mod[t, τ] <= τ/2}, {#2, True}}] &, {H1, 
   H2}, 2]

$$\left( \begin{array}{ccc} 2 & 3 & \begin{array}{cc} \{ & \begin{array}{cc} 0 & (t \bmod 0.5)\leq 0.25 \\ 4 & \text{True} \\ \end{array} \\ \end{array} \\ 3 & 2 & 0 \\ \begin{array}{cc} \{ & \begin{array}{cc} 0 & (t \bmod 0.5)\leq 0.25 \\ 4 & \text{True} \\ \end{array} \\ \end{array} & 0 & 2 \\ \end{array} \right)$$

ψ[t_] = Through[Array["ψ", 3][t]];

sol[t_] = ψ[t] /. 
   First@NDSolve[{Thread[
       I ψ'[t] == h[t].ψ[t]], ψ[0] == {0, 1, 
        0}}, ψ[t], {t, 0, n τ}];

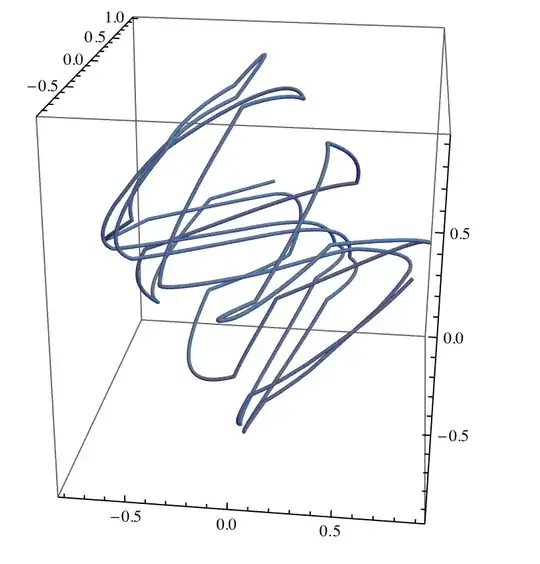
ParametricPlot3D[Re@sol[t], {t, 0, n τ}, PlotStyle -> Tube[.01]]

Jens
  • 97,245
  • 7
  • 213
  • 499
  • Thanks for your reply. Two comments...(1) If I consider n=0, then the piecewise conditions should be {{H1, 0<= t <= (1/2) τ}, {H2, (1/2) τ <= t <= τ}}. Can be solve this situation with considering total time =20 τ for the numerical solution. (2) If x is not a constant and I want to plot solution with x for given time. Is it possible? – santosh May 08 '16 at 04:39
  • I don't understand point (1) - isn't that what I have already? I used your n as the number of periods to follow, so it has no role to play inside the Piecewise because Mod takes care of subtracting the appropriate integer multiple of $\tau$. For (2), the answer is yes, you can make x time dependent without any problem. – Jens May 08 '16 at 04:46
  • I am little confuse with the mod used in the piecewise. I think it is doing the same thing as shown in my figure. [![enter image description here][1]][1]. – santosh May 08 '16 at 05:13
0

It is simple like that:

H1 = {{x, y, 0}, {y, x, 0}, {0, 0, x}};
H2 = {{x, y, z}, {y, x, 0}, {z, 0, x}};

x = 2; y = 3; z = 4;
n = 20; \[Tau] = 0.5;
HI[t_?NumericQ] := 
 Piecewise[{{H1, 
    n \[Tau] <= t <= (n + 1/2) \[Tau]}, {H2, (n + 1/2) \[Tau] <= 
     t <= (n + 1) \[Tau]}}]

NDSolve[{\[Psi][n \[Tau]] == {0, 1, 0}, 
 I \[Psi]'[t] == HI[t].\[Psi][t]}, \[Psi][t]
, {t, n \[Tau], (n + 1) \[Tau]}]
swish
  • 7,881
  • 26
  • 48