Fitting a Gaussian model to specific section of my list?

Question

I'm analysing some Decay sepctrums for a Nuclear Physics project.

I need to fit a gaussian model to a specific X-Ray peak to determine the centroid so I can get a good channel-energy calibration.

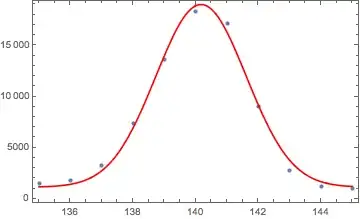
The problem is I have a list with 7000 channels but the X-Ray peak is located between channel 135 and 145. I want to fit a gaussian to this specific region in my data.

In the image below the Vertical axis corresponds to Counts while the Horizontal to Channel. This is essentially a ListLinePlot of my raw data which is a list of counts.

How do I fit a Gaussian to a specific region in my data?

Link to the data:

https://www.dropbox.com/s/dtvr7x7ooe2xx1r/137Cs_and_60co_sources_calib.mca?dl=0

If you can provide a link to your data, I'd be glad to update my answer to show Gaussian fits to your data too. — Rashid, May 11 '16 at 12:10
Thanks for the data. It looks like @BlacKow has already parsed and processed it. Please take at BlacKow's new answer and also comment above that points to another helpful answer. I think these should help you out. — Rashid, May 19 '16 at 01:34

Rashid · Answer 1 · 2016-05-11T11:54:37.020

You can use Select to choose a region of data to fit over.

Here's an example with a simple linear fit (adapted from the first case in the Fit documentation):

You can limit the fit range to a certain range of x values (e.g. x<2):

data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
wholeRangeLine = Fit[data, {1, x}, x]
shortRangeLine = Fit[Select[data, #[[1]] < 2 &], {1, x}, x]
Show[ListPlot[data, PlotStyle -> Red], 
Plot[{wholeRangeLine, shortRangeLine}, {x, 0, 5}]]

(* wholeRangeLine returns 0.186441 + 0.694915 x *)
(* shortRangeLine returns 1. - 1. x *)

You can also limit based on the y values (e.g. y>=2):

highValueLine = Fit[Select[data, #[[2]] >= 2 &], {1, x}, x]
Show[ListPlot[data, PlotStyle -> Red], 
Plot[{wholeRangeLine, highValueLine}, {x, 0, 5}]]

(* highValueLine returns -1. + 1. x *)

Hi! Here is the data! Thank you for your attention. https://www.dropbox.com/s/dtvr7x7ooe2xx1r/137Cs_and_60co_sources_calib.mca?dl=0 — Frederico Arez, May 17 '16 at 07:15

score 1 · Accepted Answer · edited Jun 16 '20 at 09:23

I'm not sure what problem you are experiencing. Here is a very straightforward way for your particular dataset. For general peak finding technique consult with the link I posted in comments.

First we read the data and skip the header:

data = #[[Position[#, "<<DATA>>"][[1, 1]] + 1 ;; -2, 1]] &@
   Import["https://www.dropbox.com/s/dtvr7x7ooe2xx1r/137Cs_and_60co_\
sources_calib.mca?dl=1&pv=1", "Table"];

Then we select appropriate region (135-145) and add x-coordinate, so we have a list of pairs that will be fed into fitting engine

regionData = 
  Transpose[{Range[#1, #2, 1], data[[#1 ;; #2]]} & @@ {135, 145}];

Now we fit the data with gaussian function (giving some expectations about our parameters)

nlm = NonlinearModelFit[
   regionData, {d + A Exp[-(t - m)^2/2/sigma^2], 138 < m < 142, 
    0 < d < 2000, 0 < sigma < 10}, {d, A, m, sigma}, t];
Show[ListPlot[regionData, PlotRange -> Full], 
 Plot[nlm[t], {t, 135, 145}, PlotStyle -> Red, PlotRange -> Full], 
 Frame -> True]
nlm["BestFitParameters"]

{d -> 1135.71, A -> 17860.1, m -> 140.169, sigma -> 1.44384}

As a side note, I don't believe this particular peak is good for calibration your MCA. You will be better with at least two peaks that are far apart in your scale. This way you will cover full scale of your device.

thank you very much! I have just started using Mathematica for data analysis so I'm still not very familiar on how things work! This is exactly what I needed!! — Frederico Arez, May 19 '16 at 10:03

Fitting a Gaussian model to specific section of my list?

2 Answers2