Plotting a manifold within an existing surface

Question

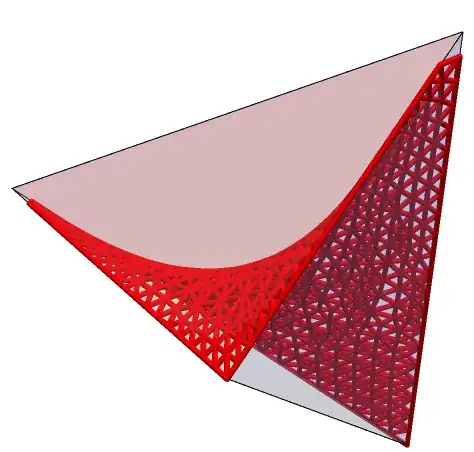
I have a dynamical system $\textbf{x}'=\textbf{f(x)}$ where $x\in \mathbb{R}^4$. However, $x_1 +x_2 +x_3 + x_4 =1$ and $0\leq x_i \leq 1$ for $i = 1,2,3,4$, meaning the system lives on the Tetrahedron.

I am trying to plot solutions to this system and the manifold implicitly given by $x_1 x_4 - x_2 x_3 =0$. This is because solutions to my system lay close to this manifold and this is a result of interest.

So far, I have been plotting on the Tetrahedron using a crude projection matrix:

$B = \left( \begin{array}{cccc} 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{\sqrt{\frac{3}{2}}}{4}+\frac{1}{4 \sqrt{6}} & \frac{\sqrt{\frac{3}{2}}}{4}+\frac{1}{4 \sqrt{6}} & -\frac{\sqrt{\frac{3}{2}}}{2}-\frac{1}{2 \sqrt{6}} \\ \frac{\sqrt{3}}{2} & -\frac{1}{2 \sqrt{3}} & -\frac{1}{2 \sqrt{3}} & -\frac{1}{2 \sqrt{3}} \\ \end{array} \right)$

I have been numerically solving my system to find a single orbit, $x(t)$. Then, by performing $B.x(t)$, I am able to visualise the solution on the simplex using:

    Show[Line[B.x[t]],Line[B.{1,0,0,0},B.{0,1,0,0},etc]]

to plot both the solution and the edges of the tetrahedron.

However, I have recently discovered

   ImplicitRegion[], DiscretizeRegion[]

and other similar functions. This has led me to believe there is a far better and more proper way of getting these plots. So far I have been able to see the $x_1 x_4 - x_2 x_3 =0$ manifold by using

    R = DiscretizeRegion[ImplicitRegion[x1 (1-x1-x2-x3) - x2 x3 ==0, {{x1,0,1},{x2,0,1},{x3,0,1}}]]

However, when I attempt to combine this with the regular tetrahedron, by using

    Show[Graphics3D[Tetrahedron[],R]

The result is a god awful mess. This is clearly because the exact projections being used are different, but I am unable to figure out how to fix this.

Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Michael E2, May 12 '16 at 17:11

xslittlegrass · Accepted Answer · 2016-05-12T19:41:22.983

5

You can combine Graphics3D and the MeshRegion using their MeshPrimitives. For example,

Show[Graphics3D[{Blue, Tetrahedron[]}], Graphics3D[{Red, MeshPrimitives[R, 1]}]]

or

Show[Graphics3D[{Opacity[0.3], Tetrahedron[]}], 
 Graphics3D[{Red, MeshPrimitives[R, 1]}] /. Line -> Tube, 
 Boxed -> False]

edited May 12 '16 at 19:41

answered May 12 '16 at 16:46

xslittlegrass

27,549
9
97
186

Plotting a manifold within an existing surface

1 Answers1