plotting a function in bipolar coordinates

Question

How to plot a function specified in bipolar coordinates if straightforward substitution of expression of Cartesian ones via them is impossible?

"a function specified in bipolar coordinates" - do you have an example on hand? — J. M.'s missing motivation, May 13 '16 at 09:11
Yes, the function I wish to see is
Sqrt[Cosh[u] - Cos[v]]/Sinh[u] !( (*SubsuperscriptBox[(f), ((-1)/2), (,)])[(Cosh[u])]) where Subscript[f, -1/2] is Legendre' s either P or Q of order - 1/2 of imaginary argument. Too complcated for a beginner. — Zafar Turakulov, May 14 '16 at 16:20

george2079 · Answer 1 · 2016-05-13T18:56:35.683

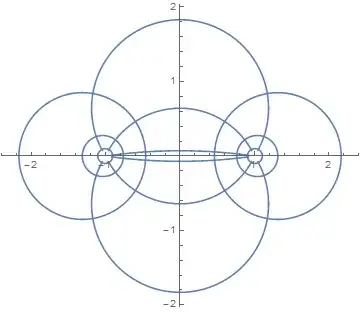
We can do this by implementing the transformation formula directly: (ref https://en.wikipedia.org/wiki/Bipolar_coordinates )

bipolar[a_] =  a {Sinh[#[[2]]], Sin[#[[1]]]}/
                     (-Cos[#[[1]]] + Cosh[#[[2]]]) &

Show[{ParametricPlot[ 
   Table[bipolar[1]@{s, t}, {t, 
     Cases[Range[-3, 3], Except[0]]}] , {s, -Pi, Pi}, 
   AspectRatio -> Automatic, PlotRange -> All],
  ParametricPlot[ 
   Table[bipolar[1]@{s, t}, {s, 
     Cases[Range[-3, 3], Except[0]]}] , {t, -Pi, Pi}, 
   AspectRatio -> Automatic, PlotRange -> All]}]

or use the built in CoordinateTransform

ParametricPlot[ 
   Evaluate[ CoordinateTransform[
         {{"Bipolar", {1}} -> "Cartesian"}, {s, 1}]] ,
            {s, -Pi, Pi}, AspectRatio -> Automatic, PlotRange -> All]]

(note Evaluate is essential here or it will be extremely slow)

Thank you very much. I try to understand what is written. – Zafar Turakulov May 14 '16 at 16:21 — Zafar Turakulov, May 14 '16 at 16:21

plotting a function in bipolar coordinates

1 Answers1