Flip sign of one variable in list

Question

I have this list of x, y-pairs l={{x1, y1}, {x2, y2}, ...}. Now I need to flip the sign of the y values only before plotting. What is the easiest way to do this modification?

{1, -1} # & /@ l or Transpose@{#[[1]], -#[[2]]} &@Transpose[l] — BlacKow, May 13 '16 at 15:39
Welcome! I suggest the following:

As you receive help, try to give it too, by answering questions in your area of expertise.

Take the tour and check the faqs!

When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — , May 13 '16 at 15:50
This is almost certainly a duplicate. I will see if I can find it. — march, May 13 '16 at 15:55

BlacKow · Answer 1 · 2016-05-16T22:21:32.807

12

Little benchmark to compare suggested methods:

l = RandomReal[{0, 1}, {1000000, 2}];
b1[l_List] := {1, -1} # & /@ l;
b2[l_List] := Transpose@{#[[1]], -#[[2]]} &@Transpose[l];
b3[l_List] := Transpose[{1, -1} Transpose[l]];
m1[l_List] := MapAt[-# &, l, {All, 2}];
m2[l_List] := {#1, -#2} & @@@ l;
ch1[l_List] := l /. {a_, b_} :> {a, -b};
g1[l_List] := l ConstantArray[{1, -1}, Length@l];
w1[l_List] := l.{{1, 0}, {0, -1}};
fb1[l_List] := Thread[{l[[;; , 1]], -l[[;; , 2]]}];

#2 -> #1 & @@@ SortBy[#, #[[1]] &] &@({#1, #2} & @@@Transpose@{First@AbsoluteTiming[#[l]] & /@ #, #}&@{b1, b2, b3,m1, m2, ch1, g1,w1,fb1})

{w1 -> 0.007054, b3 -> 0.016369, b2 -> 0.020753, b1 -> 0.155566, fb1 -> 0.25016, g1 -> 0.323931, m2 -> 1.05527, m1 -> 1.13127, ch1 -> 1.32451}

edited May 16 '16 at 22:21

answered May 13 '16 at 16:03

BlacKow

6,428
18
32

b3 is the last thing I would have used without much thinking, neat to see how much faster it is though. – N.J.Evans May 13 '16 at 16:28
@FrankBreitling Usually you create a new list in Mathematica and not modify existing one. Your method l=Thread[{l[[1]], -l[[2]]}] doesn't yield desired result. – BlacKow May 13 '16 at 17:02
you could write b3 as Transpose[{1, -1} Transpose@l] (+1) – kglr May 13 '16 at 17:59
@kglr Indeed... not sure why I came up with that one lol.. Fixed – BlacKow May 13 '16 at 18:01
... not only it is the fastest but also the shortest if you write it as ({1,-1} l):) – kglr May 13 '16 at 18:07
@kglr I can't see superscript T in Safari on Mac. – BlacKow May 13 '16 at 18:10
@BlacKow, it shows as a box in Chrome on Windows too. But if you copy/paste into mma it renders properly: 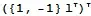– kglr May 13 '16 at 18:13
Thank you, that's very interesting! How does this compare to l=Thread[{l[[;;,1]], -l[[;;,2]]}] I had thought about? Are these methods creating new lists or just modifying the existing list which is interesting with respect to memory usage? – Frank Breitling May 15 '16 at 14:54
1

@FrankBreitling I updated my answer with your method. – BlacKow May 16 '16 at 22:21
@BlacKow Thank you very much! – Frank Breitling May 17 '16 at 09:03

score 11 · Accepted Answer · answered May 14 '16 at 01:29

11

Dot works well here.

pts = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};

pts.{{1, 0}, {0, -1}}

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

In version 10.1.0 under Windows x64 this is twice as fast as BlacKow's fastest method:

l = RandomReal[{0, 1}, {1000000, 2}];

Transpose[{1, -1} Transpose[l]]   // RepeatedTiming // First

l.{{1, 0}, {0, -1}}               // RepeatedTiming // First

0.0133
0.0072

answered May 14 '16 at 01:29

Mr.Wizard

271,378
34
587
1,371

I was so sure that you can't do this, that it will cause some dimensions mismatch, so I haven't even tried this... I'll add it to my benchmark later. Thanks! – BlacKow May 14 '16 at 03:12
1

I like this. Nice to see you using dot products! :) – J. M.'s missing motivation May 14 '16 at 05:13
@J.M. There is a pretty good chance you taught me this but my memory is too poor to remember. – Mr.Wizard May 14 '16 at 06:29
@J.M. Do you feel that this is a duplicate of (38138)? I do, but not strongly, and I did not wish to act alone. – Mr.Wizard May 15 '16 at 03:38
Somehow I recall another thread with the exact same problem of reflecting, but the link escapes me at the moment. BTW, I'm sure you know this, but for general scaling and reflection, one could use DiagonalMatrix[], or even ScalingTransform[]. – J. M.'s missing motivation May 15 '16 at 04:10

score 2 · Answer 3 · answered Jan 02 '24 at 00:08

2

list = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};

Using Threaded (new in 13.1)

list * Threaded[{1, -1}]

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

answered Jan 02 '24 at 00:08

eldo

67,911
5
60
168

score 1 · Answer 4 · answered Jan 02 '24 at 00:35

1

Using Cases and PauliMatrix[3]:

pts = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};
Cases[pts, v_ :> v . PauliMatrix[3]]
({{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}})

answered Jan 02 '24 at 00:35

E. Chan-López

23,117
3
21
44

bmf · Answer 5 · 2024-01-02T00:42:24.457

I am glad to see that people are using Threaded

I am surprised nobody mentioned the use of Inner

Grabbing the list from @eldo

list = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};

This

Inner[Times, list, {1, -1}, List]

returns

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

We can, also, use Splice

Cases[list, x_ :> {First@x, Splice@Rest@-x}]

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

And ApplyTo

list = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};
list //= ReplaceAt[x_ :> -x, {All, 2}];
list

giving

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

score 1 · Answer 6 · answered Jan 02 '24 at 01:36

1

list = {{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}};

SubsetMap[-# &, list, {All, 2}]
SequenceCases[list, {{a_, b_}} :> {a, -b}]
list . ReflectionMatrix[{0, 1}]

Result:

{{x1, -y1}, {x2, -y2}, {x3, -y3}, {x4, -y4}}

answered Jan 02 '24 at 01:36

Syed

52,495
4
30
85

Flip sign of one variable in list

6 Answers6

Linked