Fractal plotting for the Collatz fractal

Question

I have the following equation:

f[z_] := 1/4 (2 + 7 z - (2 + 5 z) Cos[Pi*z])

I want to map this on the imaginary plane such that if it converges under iterations of the function then it is plotted. I would like to then color this in a Mandelbrot type way. How would I go about plotting this?

The goal is to explore the fractal mentioned here.

This is the type of image i'm trying to produce with the ability to zoom in to particular points.

Please excuse my ignorance blase, how may I help you? Maybe I can program the whole thing for you? — , May 20 '16 at 07:57
Tweak as needed: DensityPlot[-Length[FixedPointList[Function[z, (2 + 7 z - (2 + 5 z) Cos[Pi z])/4], x + I y, 100, SameTest -> (Abs[#2] > 25. &)]], {x, -5, 5}, {y, -1, 1}, AspectRatio -> Automatic, ColorFunction -> (RGBColor[0, 0, #] &), PlotRange -> All] — J. M.'s missing motivation, May 20 '16 at 08:04
I'm always at a loss with these pictures, about what is being plotted. Nathaniel Johnston writes that the black portions of the plot are areas where the orbit is bounded (Check out the Orbit function here). But what is the color in the rest of the plot based on? — Jason B., May 20 '16 at 09:59
"but with each color representing the number of iterations required before a point is declared to not be a member of the Collatz set."
So when provable not in the set show steps takes to prove if not have a halting criteria which is the uniform background color. — shai horowitz, May 20 '16 at 10:02
The snippet I gave is essentially a naive escape-time algorithm implementation. As noted, adjust stuff as needed (e.g. PlotPoints, MaxRecursion, ColorFunction). — J. M.'s missing motivation, May 20 '16 at 13:07

score 12 · Accepted Answer · answered May 21 '16 at 17:06

One way of coding the iterations may be defined as follows. The function CollatzFractal01[z0] returns a list {Abs[z],iter}, where Abs[z] is the final value of z, and iter is the number of iterations required to escape the bound of Abs[z]>200. Use compilation and parallelisation for speed.

CollatzFractal01 = Compile[{{z0, _Complex, 0}},
   Module[{iter = 0, max = 3000, z = z0},
      While[iter++ < max, 
         If[Abs[z = (2 + 7 z - (2 + 5 z) Cos[Pi z])/4] > 200., Break[]]];
      {Abs[z], iter}],
   CompilationTarget -> "C", Parallelization -> True, 
   RuntimeAttributes -> {Listable}];

Generate a table of locations in the complex plane with ParallelTable.

d = ParallelTable[i + I*j, {j, -0.5, 0.5, 0.001}, {i, 0.3, 2.5, 0.001}];

Graphics[Raster[...]] can be faster than ArrayPlot[...]. This plot shows the final Abs[z].

Graphics[Raster[
   Rescale[Log[Log[CollatzFractal01[d][[All, All, 1]] + 1.] + 1.]],
   ColorFunction -> (ColorData["FallColors", 1 - #] &)],
   ImageSize -> 600, Background -> Black]

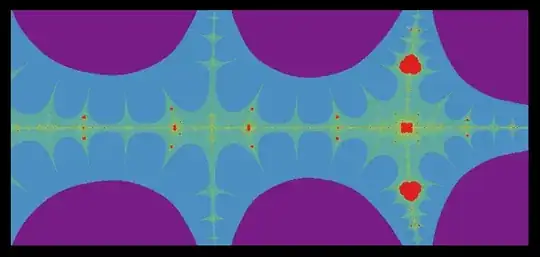
This plot shows the number of iterations.

Graphics[Raster[
   Rescale[Log[Log[CollatzFractal01[d][[All, All, 2]] + 1.] + 1.]],
   ColorFunction -> (ColorData["Rainbow", #^0.5] &)],
   ImageSize -> 600, Background -> Black]

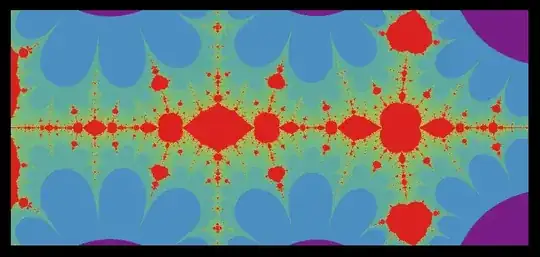
Slightly redefining your original equation gives more "interesting" plots, with far more structure. However, the calculation time increases substantially.

CollatzFractal02 = Compile[{{z0, _Complex, 0}},
   Module[{iter = 0, max = 3000, z = z0},
      While[iter++ < max, 
         If[Abs[z = (1 + 4 z - (1 + 2 z) Cos[Pi z])/4] > 200., Break[]]];
      {Abs[z], iter}],
   CompilationTarget -> "C", Parallelization -> True, 
   RuntimeAttributes -> {Listable}];

The iteration count for example:

Only slightly slower: DensityPlot[Log[1 + Log[Length[FixedPointList[Function[z, (2 + 7 z - (2 + 5 z) Cos[Pi z])/4], x + I y, 3*^3, SameTest -> (Abs[#2] > 200. &)]]]], {x, 1/3, 5/2}, {y, -1/2, 1/2}, AspectRatio -> Automatic, ColorFunction -> (ColorData["Rainbow", Sqrt[#]] &), PlotPoints -> 145, PlotRange -> All] — J. M.'s missing motivation, May 21 '16 at 17:24

Fractal plotting for the Collatz fractal

1 Answers1