Comparing LetL and Module efficiency

Question

I was recently introduced to the LetL macro thanks to Leonid's answer to one of my prior questions. I was, needless to say, impressed by the simplicity of its recursive definition. However, I noticed that it may not necessarily be optimized. As it is defined, if my LetL statement contains a definition which does not need to be nested, then it will call With unnecessarily:

testLetL := LetL[{x = 1, y = 2, z = 2 x y}, {x, y, z}]
?testLetL
(* testLetL:=With[{x=1},With[{y=2},With[{z=2 x y},{x,y,z}]]] *)

So I compared it to Module:

testModule := Module[{x = 1, y = 2, z}, z = 2 x y; {x, y, z}]
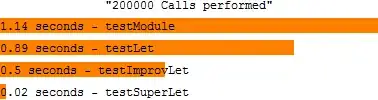
(Do[#, {i, 5000000}] // AbsoluteTiming) & /@ {testLetL, testModule}
(* {{0.9390537, Null}, {0.9270530, Null}} *)

As you can see, there doesn't seem to be much speed gained in using LetL - essentially nested Withs - instead of Module. I thought perhaps that it was the extra With being called that was slowing things down. So I tried another test:

testLetL2 := LetL[{x = 1, y = 2 x }, {x, y}]
testModule2 := Module[{x = 1, y}, y = 2 x ; {x, y}]
(Do[#, {i, 5000000}] // AbsoluteTiming) & /@ {testLetL2, testModule2}
(* {{0.9270531, Null}, {0.9120521, Null}} *)

This again showed that they were pretty much the same, if not Module being a bit faster.

---

My question is, then:

Is LetL simply used for convenience or are my tests missing something?

Answer 1

The main point of LetL is just replacement of nested With, not necessarily the speed gain. Now, why would one want to use nested With in place of Module:

• Immutable code (same advantages as With - no side effects in the body)
• Use variables defined earlier in definitions of variables defined later.

In fact, if you want the second property, you will either have to have nested Module-s as well, or make side effects in the body.

That said, LetL should be pretty fast. You should not normally see large timing difference between LetL and equivalent nested With. Moreover, for functions defined via SetDelayed, LetL expands into equivalent nested With at definition-time, so there is no run-time performance penalty at all.

And yes, your tests missed the point, since pure function is #-& notation evaluates its argument, so you were actually testing already evaluated expressions. Try this:

Do[testLetL2,{i,50000}]//AbsoluteTiming
Do[testModule2,{i,50000}]//AbsoluteTiming

(*
   {0.190430,Null}
   {0.276367,Null}
*)

Answer 2

I'd like to add to this post that there are performance gains to be found in intelligently positioning you'r nested With statements. To take your example if we have the following definitions and code:

 {x = 1, y = 2, z = 2 x y}, {x, y, z}

We can either use a Module, naively use 3 nested With's, or though analyzing the structure of the definitions we can see that we can get away with just two Withs, and then we can be really smart about our optimization (to be explained after performance results for dramatic effect!). So here's the results of these methods:

testModule := Module[{x = 1, y = 2, z}, z = 2 x y; {x, y, z}];
testLet := With[{x = 1}, With[{y = 2}, With[{z = 2 x y}, {x, y, z}]]];
testImprovLet := With[{x = 1, y = 2}, With[{z = 2 x y}, {x, y, z}]];

On my system, calling these three and the to be described testSuperLet gives the following results:

So in short, With is faster than Module for this test, and trying to minimize the levels of With's does help improve the speed significantly. But all of these are nothing compared to superLet, so let's get to it. What is `superLet? Well if you look at the test again, you'll notice that we don't actually need to recalculate anything since it's just providing a constant, so the best way to nest the with's is to just move them left of the definition:

With[{x = 1, y = 2}, With[{z = 2 x y}, testSuperLet := {x, y, z}]]

I know I know, it looks like cheating, however in many cases, using your definitions outside of the Set/SetDelayed can provide significant improvements in speed with only a slight cost in DownValue size and complexity.

The code used to generate the timing graph above:

SetAttributes[time,HoldAll]
time[code_,num_]:=(Do[code,{num}];//AbsoluteTiming//First)
bar[n_,v_]:=Overlay[{Pane["",BaseStyle-> Background->Orange,ImageSize-> Scaled[v]],Pane[n]}]

SetAttributes[timeTableView,HoldAll]
timeTableView[calls___,num_Integer]:=Module[{labels,times},
labels=List@@(Function[a,SymbolName[Unevaluated[a]],HoldAll]/@Hold[calls]);
times=List@@(time/@Hold[calls]);
Labeled[
Column[bar[ToString[#[[2]]]<> " seconds - "<>#[[1]],#    [[3]]]&/@({labels,Round[times,0.01],times/Max[times]}\[Transpose]),ItemSize-> {30}],
ToString[num]<>" Calls performed",Top]
]

timeTableView[testModule, testLet, testImprovLet, testSuperLet, 200000]