How do I prevent Root and RootSum from expanding over quadratic roots?

Question

For cubic and higher order polynomials, Root and RootSum are generally left unevaluated:

RootSum[d + c #1 + b #1^2 + a #1^3 &, Cos[#1] &]

RootSum[d + c #1 + b #1^2 + a #1^3 &, Cos[#1] &]

But for sum over roots of quadratic and lower order polynomials,

RootSum[a #^2 + b # + c &, Cos[#] &]

immediately turns into

and also,

Root[a #^2 + b # + c &, 1]
Root[a #^2 + b # + c &, 2]

each immediately get turned into (- case for 1 and + case for 2)

This is bad for two reasons:

For numeric evaluation, forms that are output by Root are not the best (e.g. it is sometimes more stable to write the second root x2 in terms of the first x1 using x2 -> c/a*1/x1).
Analytically, if the coefficients a, b, c are generally complicated expressions, it is more compact and also more pleasant to the eye if the expression is left in RootSum or Root from.

Question: How do I prevent the automatic expansion of Root and RootSum over quadratic roots, and force them to remain unevaluated/unexpanded like for higher order polynomials.

None of the evaluation control functions Hold, Unevaluated, Inactive... are acceptable here since they interfere with symbolic manipulation routines that would otherwise work without them, e.g.:

D[Inactive[RootSum][a #^2 + b # + c &, Cos[ω #] &], ω]

The ideal solution would entail either setting specific options to Root or RootSum to prevent automatic expansion, or to modify (possibly undocumented) internal code associated with these functions.

Can you explain what form you would like the RootSum to appear in? — bill s, Sep 27 '16 at 01:06
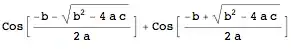
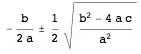
@bills I edited my question. Essentially, I want Root and RootSum to remain unexpanded for generic quadratic and lower order polynomials. i.e RootSum[a #^2 + b # + c &, Cos[#] &] should return unevaluated just as RootSum[a #^3 + b #^2 + c # + d &, Cos[#] &] is returned unevaluated. — QuantumDot, Sep 27 '16 at 01:12
It does not seem to do the expansion if the function is general -- i.e., RootSum[d + c # + b #^2 &, f] is not expanded. — bill s, Sep 27 '16 at 01:38
I do not understand why, for instance, Inactive is unacceptable. D[Inactive[RootSum][a #^2 + b # + c &, Cos[ω #] &], ω] // Activate works well. The only downside I see is that Inactive needs to be applied in each operation. It is for that reason only that I suggest Defer instead. — bbgodfrey, Sep 28 '16 at 04:05

score 2 · Answer 1 · edited Apr 13 '17 at 12:55

The following may help. According to its documentation, "Defer[expr] yields an object that displays as the unevaluated form of expr, but that is evaluated if it is explicitly given as Wolfram Language input."

Defer[RootSum[a #^2 + b # + c &, Cos[ω #] &]]

(* RootSum[a #1^2 + b #1 + c &, Cos[ω #1] &] *)

But,

D[%, ω] /. Defer'[_] -> 1

(* -(((-b - Sqrt[b^2 - 4 a c]) Sin[((-b - Sqrt[b^2 - 4 a c]) ω)/(2 a)])/(2 a)) 
   - ((-b + Sqrt[b^2 - 4 a c]) Sin[((-b + Sqrt[b^2 - 4 a c]) ω)/(2 a)])/(2 a) *)

as desired.

Addendum

A cleaner approach, based on an answer by Mr.Wizard, is

D[%, ω] // ToBoxes // ToExpression

How do I prevent Root and RootSum from expanding over quadratic roots?

1 Answers1