ClearAll["Global`*"];
Remove["Global`*"];
sol = NDSolve[{f''[x] == f[x]^3 - f[x], f[-3] == 1, f[3] == -1}, f[x], {x, -3, 3},
Method -> {"Shooting", "StartingInitialConditions" -> {f'[0] == 0, f[0] == 1}}];
UPDATE:
Maples symbolic solution(The symbolic solution is quite long and complex) ,converted to numeric form.Maple gives 5 solutions other than Mathematica.

Maples JacobiSN[z,k] is equal to Mathematica JacobiSN[z,k^2].
With 20 digits precision.
maple1 = (-1.5279997865913399554 - 0.58636062345487262098*I)*
JacobiSN[(0.94894046904339260202 -
0.94416766565747605255*I)*(0.70710678118654752440*x +
1.6985155326343786960 -
0.20793350722877537103*I), (-0.50021641106619559220 -
1.1156113783217666782*I)^2];
maple2 = (-0.57150532368340334446 -
0.87200104339127158745*I)*
JacobiSN[(1.5911818830635583675 -
0.31319690342130914617*I)*(0.70710678118654752440*x +
1.7471798211151876014 +
0.44795429731942814652*I), (-0.24192870056640322887 -
0.59564049424232431474*I)^2];
maple3 = (-1.5279997865913399554 -
0.58636062345487262098*I)*
JacobiSN[(0.94894046904339260202 -
0.94416766565747605255*I)*(0.70710678118654752440*x +
1.6985155326343786960 -
0.20793350722877537103*I), (-0.50021641106619559220 -
1.1156113783217666782*I)^2];
maple4 = (-1.5279997865913399554 -
0.58636062345487262098*I)*
JacobiSN[(0.94894046904339260202 -
0.94416766565747605255*I)*(0.70710678118654752440*x +
1.6985155326343786960 -
0.20793350722877537103*I), (-0.50021641106619559220 -
1.1156113783217666782*I)^2];
maple5 = (-1.5279997865913399554 +
0.58636062345487262098*I)*
JacobiSN[(0.94894046904339260202 +
0.94416766565747605255*I)*(0.70710678118654752440*x +
1.6985155326343786960 +
0.20793350722877537103*I), (-0.50021641106619559220 +
1.1156113783217666782*I)^2];
.
Boundary conditions check:
Re[{maple1, maple2, maple3, maple4, maple5}] /. x -> -3 // N
(*{1., 1., 1., 1., 1.}*)
Re[{maple1, maple2, maple3, maple4, maple5}] /. x -> 3 // N
(*{-1., -1., -1., -1., -1.}*)
.
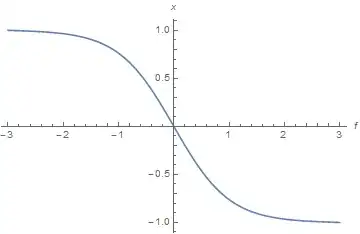
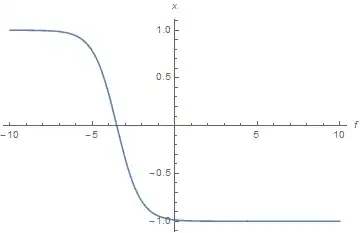
Plot[{Re[maple1], Re[maple2], Re[maple2], Re[maple2], Re[maple2],
f[x] /. sol}, {x, -3, 3},
PlotLegends -> {"maple1", "maple2", "maple3", "maple4", "maple5",
"NDSOLVE"},
PlotStyle -> {Red, {Green, Dashing[{0.2, 0.05}],
Thickness[0.01]}, {Blue, Thickness[0.01],
Dashing[{0.3, 0.1}]}, {Black, Thickness[0.01],
Dashing[{0.1, 0.1}]}, Yellow, Brown}, AxesLabel -> {x, f[x]}]




Tanh?FullSimplify[(f''[x] - f[x]^3 + f[x]) /. {f -> Function[{x}, Tanh[x]]}] = -Sech[x]^2 Tanh[x]– mattiav27 May 29 '16 at 12:05FullSimplify[Tanh[x]^3 - Tanh[x]]==-Sech[x]^2 Tanh[x]. You miss a factor 2 in the RHS of your equation. – mattiav27 May 29 '16 at 12:49fff = NDSolve[{f''[x] == 2 (f[x]^3 - f[x]), f[-3] == 1, f[3] == -1}, f[x], {x, -3, 3}, Method -> "StiffnessSwitching"]NDSolve::ndsz: At x == 0.3758850281121969`, step size is effectively zero; singularity or stiff system suspected. – satoru May 29 '16 at 12:56NDSolvesince one can get exact solutions withDSolve? – Artes May 29 '16 at 13:47DSolvegives me a solution (in terms ofJacobiSN), only when I discard the boundary conditions, in which case I am left with two unknown constants that are not easy to evaluate. Have you done better? Thanks. – bbgodfrey May 29 '16 at 16:37JacobiSN's yields solutions in terms ofTanh. I wish the original poster would clearly point out the actual problem. – Artes May 29 '16 at 17:01C[1] == 1andC[2] == 0. Thanks. The OP gave his actual question in a comment to my answer below, and I then added a sample calculation of it to my answer. However, I have not tried to obtain results for largerα. – bbgodfrey May 29 '16 at 17:15Tanh[]is actually whatJacobiSN[]will degenerate to if its second argument is1, FYI. – J. M.'s missing motivation May 29 '16 at 17:22