3

I've been playing around with some d-orbitals and have been trying to view their maximum in two dimensions. At the moment I've progressed to the point where the d__ orbitals are superimposed onto one another, in 2d, using a modification of Jens' answer here but have not managed to obtain the outline. Please pardon the code, its probably a bit convoluted and ever so slightly messy:

{rMin[n_, l_], rMax[n_, l_]} = r /. Simplify[Solve[(l (l + 1))/r^2 - 2/r == -(1/n^2), r], n > 0];

sphericalToCartesian = Thread[{r, θ, ϕ} -> {Sqrt[x^2 + y^2 + z^2], ArcCos[z/Sqrt[x^2 + y^2 + z^2]], Arg[x + I y]}];

(*The radial orbitals here are approximated using a Slater-type orbital using Clementi's atomic constants for Fe; see Slater-type orbitals on Wikipedia for further information*)
pimp[n_, l_, m_][r_, θ_, ϕ_] := (2*22.27)^n ((2*22.27)/(2 n)!) (r^(n - 1)) (E^(-22.27 r)) (Im[SphericalHarmonicY[l, m, θ, ϕ]] + Im[SphericalHarmonicY[l, -m, θ, ϕ]])
pimn[n_, l_, m_][r_, θ_, ϕ_] := (2*22.27)^n ((2*22.27)/(2 n)!) (r^(n - 1)) (E^(-22.27 r)) (Im[SphericalHarmonicY[l, m, θ, ϕ]] - Im[SphericalHarmonicY[l, -m, θ, ϕ]])
prep[n_, l_, m_][r_, θ_, ϕ_] := (2*22.27)^n ((2*22.27)/(2 n)!) (r^(n - 1)) (E^(-22.27 r)) (Re[SphericalHarmonicY[l, m, θ, ϕ]] + Re[SphericalHarmonicY[l, -m, θ, ϕ]])
pren[n_, l_, m_][r_, θ_, ϕ_] := (2*22.27)^n ((2*22.27)/(2 n)!) (r^(n - 1)) (E^(-22.27 r)) (Re[SphericalHarmonicY[l, m, θ, ϕ]] - Re[SphericalHarmonicY[l, -m, θ, ϕ]])

(*To get a 2d plot, I set the earlier evaluation so that x->0*)
plot2dx0[f_, range_, contour_, opt : OptionsPattern[]] := RegionPlot[Evaluate[Abs[f[r, θ, ϕ] /. sphericalToCartesian]^2 >contour] /. x -> 0, {y, -range, range}, {z, -range, range}]

(*Plotting the different d-orbitals*)
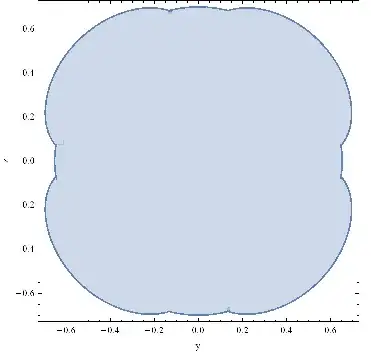
Show[plot2dx0[prep[3, 2, 0], 0.7, 0.00007], plot2dx0[pimp[3, 2, 1], 0.7, 0.00007], plot2dx0[pimn[3, 2, 2], 0.7, 0.00007], plot2dx0[pren[3, 2, 1], 0.7, 0.00007], plot2dx0[prep[3, 2, 2], 0.7, 0.00007], Frame -> True, FrameLabel -> {"y", "z"}]

(*Output*)

enter image description here

My question is then, whether it would be possible to (and how computational intensive would it be):

  1. Obtain only the outline of this plot for visualisation so that the distance of this outline from the centre can be quantified (probably from pi to pi/2)
  2. Plotting as a 2d density plot

For 1, it should look like:

enter image description here

For 1 & 2 I've tried the following which doesn't seem to work, and also summation of the terms (I've lost the code for that as the .nb didn't seem to save correctly on the train).

Evaluate[Max[{Abs[prep[3, 2, 0][1.12*r, θ, ϕ] /. sphericalToCartesian^2 > 0.0007],Abs[pimp[3, 2, 1][0.8*r, θ, ϕ] /. sphericalToCartesian^2 > 0.0007],Abs[pimn[3, 2, 2][1.12*r, θ, ϕ] /. sphericalToCartesian^2 > 0.0007],Abs[pren[3, 2, 1][1.12*r, θ, ϕ] /. sphericalToCartesian^2 > 0.0007],Abs[prep[3, 2, 2][1.12*r, θ, ϕ] /. sphericalToCartesian^2 > 0.0007]}]]

Could anyone please help/advise?

Many thanks, Z.

Community
  • 1
Letshin
  • 475
  • 2
  • 9

1 Answers1

4

Here is a way to do it based on Jens' answer.

sphericalToCartesian = Thread[{r, θ, ϕ} -> {Sqrt[x^2 + y^2 + z^2], 
                        ArcCos[z/Sqrt[x^2 + y^2 + z^2]], Arg[x + I y]}];

(*Atomic Orbitals*)
Ψ[n_, l_, m_][r_, θ_, ϕ_] := 
  Sqrt[(n - l - 1)!/(n + l)!] E^(-(r/n)) ((2 r)/n)^l 2/n^2 LaguerreL[
  n - l - 1, 2 l + 1, (2 r)/n] SphericalHarmonicY[l, m, θ, ϕ];

psi[n_, l_, m_][x_, y_, z_] = Ψ[n, l, m][r, θ, ϕ] /.sphericalToCartesian;

By definition, a wavefunction is spanned over all space. So what I am going to do is choose a trial value of the probability and plot its projection on a particular plane.

Lets choose $|\Psi[3,1,0]|^2=0.005$ at $x=0$ plane .

ContourPlot[Abs[psi[3, 1, 0][0, y, z]] == 0.005,
              {y, -20, 20}, {z, -20, 20}, MaxRecursion -> 5]

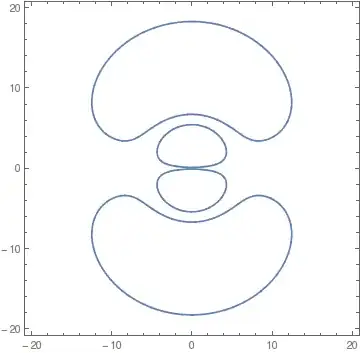
cross-section

To get the optimum value for the probability you can use Jens' {rMin,rMax} with the radial part

{rMin[n_, l_], rMax[n_, l_]} = r /. Simplify[Solve[(l (l + 1))/r^2 
                                - 2/r == -(1/n^2), r], n > 0];
pMax[n_,l_] = Abs[Ψ[n, l, 0][rMax[n,l], 0, 0]];

pMax[3,1]//N

0.00644596

Jens
  • 97,245
  • 7
  • 213
  • 499
Sumit
  • 15,912
  • 2
  • 31
  • 73
  • Thanks @J.M. for the correction before Jens saw that :) – Sumit Jun 02 '16 at 12:28
  • Now that comment made me curious... – Jens Jun 02 '16 at 14:23
  • 1
    @Jens, I'll keep that in mind the next time I need to use your name in the possessive form. (OTOH, the rule I'm accustomed to uses 's for most singular nouns even when they end in s, with a few notable exceptions.) – J. M.'s missing motivation Jun 02 '16 at 14:42
  • Many thanks for the answer. In the context of your answer, would it be possible to obtain the outline of superimposed plots (say, combining psi[3, 1, 0], psi[3, 1, 1] and psi[3, 1, 2]); that is, the maximum of the d__ orbitals at any one point (as seen in the attached image above), or to stack the d__ orbitals on top of one another, thereby forming a 'density' plot?

    @Jens... Oops, I made the mistake of the confused apostrophe as well :( Sorry...

     – Letshin Jun 02 '16 at 17:31
  • DensityPlot[Abs[ psi[n1, l1, 0][0, y, z] + psi[n2, l2, 0][0, y, z] ], ...] should work. You can use different weight for each wavefunction if you want. – Sumit Jun 03 '16 at 11:37