Plotting the solution of $\sin(x)\sin(y)$ + elliptic cylinder

Question

I have a problem with one of my school project :(

I need to add function: $\sin(x)\sin(y)$ to elliptic cylinder $\left(\frac x a\right)^2+ \left(\frac y b\right)^2 = 1$

After few hours, only this works:

f1[x_, y_] = Sin[x] Sin[y]
Plot3D[{z /. Solve[(x/5)^2 + (z/3)^2 == 1, z], f1[x, y]}, 
        {x, -10, 10}, {y, -9, 9}]

Close enough! I am trying to make cylinder go upright, because after that I had to animate a point following a $\sin(x)\sin(y)$ path on a cylinder. I don't know how to change cylinder position, any suggestion?

It's a second time I am using this program and it's not easy to do it. Can you help me?

Answer 1

I am not entirely sure what the aim is here. I am choosing a different ellipse. However, this could be easily changed.

p3 = Plot3D[Sin[x] Sin[y], {x, -5, 5}, {y, -5, 5}, 
   PlotStyle -> {Green, Opacity[0.5]}, Mesh -> False];
cp = ContourPlot3D[
   x^2/25 + y^2/9 == 1, {x, -5, 5}, {y, -5, 5}, {z, -1, 1}, 
   Mesh -> None, ContourStyle -> Opacity[0.8]];
pp = ParametricPlot3D[{5 Cos[t], 3 Sin[t], 
    Sin[5 Cos[t]] Sin[3 Sin[t]]}, {t, 0, 2 Pi}];
Manipulate[
 Show[cp, ##] &@{p}, {{p, {}}, {p3, pp}, CheckboxBar}]

Answer 2

For changing the position of the cylinder you could add a dynamic Slider. Regard that "Show" won't work within "Dynamic", so thats why I wrote the trigonometric function in the contour argument.

dx = 0;
dz = 0;
Row[{Slider2D[Dynamic[{dx, dz}], {{-10, -10}, {10, 10}}],
"dx =" Dynamic[dx], ", dz =" Dynamic[dz]}]

Dynamic[ContourPlot3D[{((x + dx)/5)^2 + ((z + dz)/3)^2 == 1, 
z == Sin[x] Sin[y]}, {x, -10, 10}, {y, -10, 10}, {z, -10, 10}, 
ContourStyle -> LightBlue, AxesLabel -> {"x", "y", "z"}]]

Answer 3

You might look into ContourPlot3D:

p1 = ContourPlot3D[(x/5)^2 + (y/3)^2 == 1, {x, -10, 10}, {y, -10, 
10}, {z, -10, 10}, ContourStyle -> LightBlue];
p2 = Plot3D[Sin[x] Sin[y], {x, -10, 10}, {y, -10, 10}];
Show[p1, p2]

Of course, if you want to do a little more with this, it helps to put both in a contourplot.

So, how do we get the intersection of the two objects? We can find a parametrization of path. After all, z only appears in one of the equations, the other equation, a cylinder is easily parametrized:

$$\left(\cos{u}, \sin{u}, v\right)｜0\le u \le 2\pi \wedge -\infty \le v \le \infty$$

Gives a nice parametrization for the cylinder, plugging in the the sine function for z, gives us the path:

$$\left(\cos{u}, \sin{u}, \sin{(5 \cos{u})} \sin{(3 \sin{u})}\right)｜0\le u \le 2\pi$$

We can now animate the point:

Manipulate[Show[p1, Graphics3D[{PointSize[0.03], 
Point[Dynamic[{5 Cos[u], 3 Sin[u], Sin[5 Cos[u]] Sin[3 Sin[u]]}]]}]], {u, 0, 2 \[Pi]}]

Answer 4

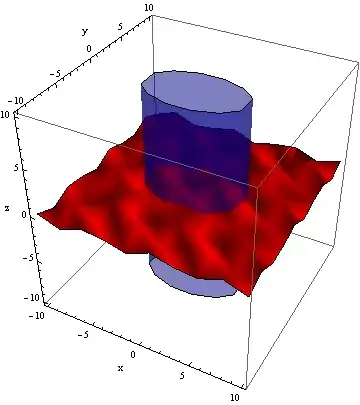
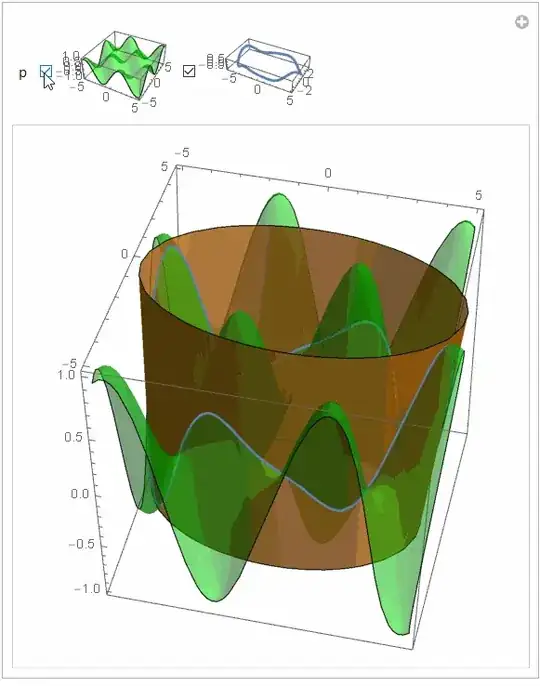
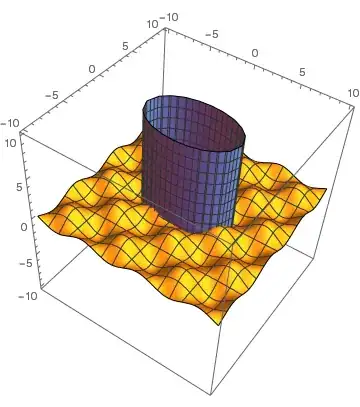
In addition I added a point animation and observed some oddly behaviour of Dynamic and ContourPlot3D.

Functions and Conditions. yPath has to be defined immidiately (without ":") cause the later \ recursive defintion wouldn' t work otherwise

yPath[x_] = -((3 Sqrt[25 - x^2])/5);
zPath[x_] := Sin[x] Sin[yPath[x]]
comparison[x_] := yPath[x] == (-yPath[x])

Coordinates of the point (Sphere)

coords[x_] := {x, yPath[x], zPath[x]}
dx[x_] := coords[x][[1]]
dy[x_] := coords[x][[2]]
dz[x_] := coords[x][[3]]

Start position of the point an steps

xi = 3;
animationSteps = {0, 1, 2, 3, 4, 5, 4, 3, 2, 1, 
0, -1, -2, -3, -4, -5, -4, -3, -2, -1};

The Plot with the dynamic output you HAVE TO SEE ON YOUR SCREEN while manipulating.

Grid[{
{ 
Animate[Row[{"xi = ", xi = step}], {step, animationSteps}, 
AnimationRunning -> False], 

Column[{Text[
"It is crazy, but you have to see the dynamic output (here \
below the text) on the screen while manipulating or the sphere will \
just be on one side of the cylinder (Mathematica 8)"], 
granted = 0,
Dynamic[ If[comparison[xi] && granted == 0, {yPath[x_] = (-1)*yPath[x], 
granted = 1}]],
Dynamic[If[comparison[xi], , granted = 0]]}]
},
{
Dynamic[ContourPlot3D[{
  (*Cylinder *)
  (xCont/5)^2 + (yCont/3)^2 == 1,
  (*Trigonometric Layer *)
  zCont == Sin[xCont] Sin[yCont],
  (*Point/Sphere *)
  (xCont - dx[xi])^2 + (yCont - dy[xi])^2 + (zCont - dz[xi])^2 == 
   3},
 {xCont, -10, 10}, {yCont, -10, 10}, {zCont, -5, 5}, 
 ContourStyle -> {Blue, Red, Black}, 
 AxesLabel -> {"x", "y", "z"} , PerformanceGoal -> "Speed", 
 ImageSize -> 300]]
}
}]

And as Gif with slitly other code instead of the Grid part

plot[xi_] := ContourPlot3D[{
(*Cylinder *)
(xCont/5)^2 + (yCont/3)^2 == 1,
(*Trigonometric Layer *)
zCont == Sin[xCont] Sin[yCont],
(*Point/Sphere *)
(xCont - dx[xi])^2 + (yCont - dy[xi])^2 + (zCont - dz[xi])^2 == 
 0.5},
{xCont, -10, 10}, {yCont, -10, 10}, {zCont, -5, 5}, 
ContourStyle -> {{Blue, Opacity -> 0.5}, Red, Black}, 
AxesLabel -> {"x", "y", "z"} , PerformanceGoal -> "Quality", 
ImageSize -> 300]

granted = 0
Dynamic[If[
comparison[xi] && granted == 0, {yPath[x_] = (-1)*yPath[x], 
granted = 1}]]
Dynamic[If[comparison[xi], , granted = 0]]

Export[NotebookDirectory[] <> "OverlapAnimation.gif", 
Table[plot[xi = animationSteps[[i]]], {i, Length[animationSteps]}]]

Some odd bahviour of ContourPlot3D:

If one of the limits - 5 or 5 is reached,the "ContourPlot3D" will oddly set its variables to its limits. So it sets here unauthorized x = 10, y = 10 and z = 10. Thats why I renamed the variables unique for ContourPlot3D in the code above

Remove["Global`*"]
yPath[x_] = -((3 Sqrt[25 - x^2])/5);
zPath[x_] := Sin[x] Sin[yPath[x]]
comparison[x2_] := yPath[x2] == (-yPath[x2]);
coords[x2_] := 
If[comparison[x2], {x2, yPath[x2], zPath[x2], 
yPath[x_] = (-1)*yPath[x]}, {x2, yPath[x2], zPath[x2]}]

dx[x_] := coords[x][[1]]
dy[x_] := coords[x][[2]]
dz[x_] := coords[x][[3]]
xi = 3;

Dynamic[ContourPlot3D[{(x/5)^2 + (y/3)^2 == 1, 
z == Sin[x] Sin[
  y], (x - dx[xi])^2 + (y - dy[xi])^2 + (z - dz[xi])^2 == 
3}, {x, -10, 10}, {y, -10, 10}, {z, -10, 10}, 
ContourStyle -> {{Blue, Opacity[0.5]}, Red, Black}, 
AxesLabel -> {"x", "y", "z"} , PerformanceGoal -> "Speed"]]

{Slider[Dynamic[xi], {-5, 5}], Dynamic[xi]}

x will become defined unauthorized and so the sphrere will wanish in the plot

x