Joining points into 3D surface

Question

This seems like a simple problem, but I can't find any questions like it here so I'm making a new one. Apologies if I missed one.

I have a list of points contained in a file which can be visualized like so:

data = Import["http://www.sharecsv.com/dl/782ae64cbc8003d67f4ab98d784015d6/data.csv"];
{a, b} = {data[[1 ;; 335]], data[[336 ;; -1]]};
ListPointPlot3D[{a, b}, PlotStyle -> {Red, Blue}]

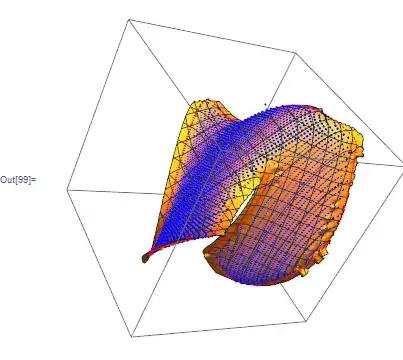
The problem is connecting/interpolating these points into a surface, ListSurfacePlot3D[] yields a garbled mess for any MaxPlotPoints.

ListSurfacePlot3D[data]

How can I transform this set of points into a (smooth) surface?

Update:

Alright fellas I'm nearly there. The best way I have come up with is to use DelaunayMesh with RunnyKine's code to produce concave meshes here. First I split the data points into non-overlapping sections by a plane between them. This is a naff hack but what can you do. Then I construct a 2D mesh for the top and bottom halves, replacing the third coordinate with Dispatch.

alphaShapes2D[points_,crit_]:=Module[{alphacriteria,del=Quiet@DelaunayMesh@points,tetras,tetcoords,tetradii,selectExternalFaces},alphacriteria[tetrahedra_,radii_,rmax_]:=Pick[tetrahedra,UnitStep@Subtract[rmax,radii],1];
selectExternalFaces[facets_]:=MeshRegion[points,facets];
If[Head[del]===EmptyRegion,del,tetras=MeshCells[del,2];
tetcoords=MeshPrimitives[del,2][[All,1]];
tetradii=Quiet@Thread[Circumsphere[tetcoords]][[All,2]];
selectExternalFaces@alphacriteria[tetras,tetradii,crit]]];

data=Standardize@Import["http://www.sharecsv.com/dl/782ae64cbc8003d67f4ab98d784015d6/data.csv"];
{a,b}={data[[1;;335]],data[[336;;-1]]};
{bot, top} = {True, False} /. GroupBy[data, Last@# < .25 First@#&];
bottri=MeshPrimitives[alphaShapes2D[bot[[All,{1,2}]],.1],2][[All,1]]/.Dispatch[#[[{1,2}]]->#&/@bot];
toptri=MeshPrimitives[alphaShapes2D[top[[All,{1,2}]],.1],2][[All,1]]/.Dispatch[#[[{1,2}]]->#&/@top];
out=Graphics3D[{Polygon/@bottri,Polygon/@toptri}]

Now I'm just missing a way to replace the missing polygons. It would have been much better to cut the data along vertices belonging to both sets. Is there a simple way you can envisage doing this?

Thank you very much for providing the points at the outset; a lot of people don't do that. If I may, where'd these points come from? — J. M.'s missing motivation, Jun 06 '16 at 07:47
Some very messy and inelegant code. I'm looking at fixed points in random 2D vector fields. Here the data[[All,3]] axis is one coordinate of a particular fixed point and the data[[All,{1,2}]] axes map out the domain that fixed point exists. I think Mathematica is getting tripped up by the bifurcation resulting in a fold in the surface. — Crêpo, Jun 06 '16 at 07:55
do you have access to the algorithm that generated the data, or just the raw points? It looks like its got a regular grid structure to it and if you had that grid info it would be useful. — george2079, Jun 06 '16 at 12:15
I generated the data by first creating the boundary points, and then sampling uniformly in the data[[All,{1,2}]] plane. In principle I can generate as many points in whatever arrangement I want, although it doesn't seem to improve the result. — Crêpo, Jun 06 '16 at 12:34
I added a figure from a different viewpoint to show this is a single simple smooth surface. — george2079, Jun 06 '16 at 14:15
@J.M. I think this problem belongs to the surface re-construction. However, the data of OP is not the style like $m \times n $ array, so I cannot apply the NURBS theory to deal with it. Wha's your viewpoints about this problem? — xyz, Jun 06 '16 at 14:50
Yes, the data is not very structured, @Shutao, so unless I'm missing any trick, NURBS does not apply here. — J. M.'s missing motivation, Jun 06 '16 at 14:55

score 10 · Answer 1 · answered Jun 06 '16 at 09:53

Not sure how useful will this be. Usually Standardize-d data is giving better results.

We can also cut off parts of the surface which are distant from our data.

rf = Nearest[Standardize@data]

sr = ListSurfacePlot3D[Standardize @ data, 
  BoxRatios -> 1, 
  MaxPlotPoints -> 100, 
  RegionFunction -> Function[{x, y, z}, 
    Norm[{x, y, z} - rf[{x, y, z}][[1]]] < .2]
]

m = Mean @ data
sd = StandardDeviation @ data


Show[
 Graphics3D[
  GeometricTransformation[
   First@sr,
   TranslationTransform[m]@*ScalingTransform[sd]
   ]
  ]
 ,
 ListPointPlot3D[{a, b}, PlotStyle -> {Red, Blue}  ]
 ,
 SphericalRegion -> True, BoxRatios -> 1
 ]

I think the main problem for the sr in your answer is smoothness. — xyz, Jun 06 '16 at 14:31
@ShutaoTANG don't claim it is best approach, but it is 1 line and looks way better than original approach. — Kuba, Jun 06 '16 at 14:32

score 7 · Accepted Answer · answered Jun 06 '16 at 15:43

I think your best bet is to generate a triangualted polygon surface. Here is an initial stab at it:

p2d = b[[All, 1 ;; 2]];
tri1[i_, j_] := 
 If[EvenQ[j], {{i, j}, {i + 1, j}, {i + 1/2, j + 1}} .05, {{i + 1/2, 
     j}, {i + 1 + 1/2, j}, {i + 1, j + 1}} .05]
tri2[i_, j_] := 
 If[EvenQ[j], {{i, j}, {i + 1, j}, {i + 1/2, j - 1}} .05, {{i + 1/2, 
     j}, {i + 1 + 1/2, j}, {i + 1, j - 1}} .05]
triangles = 
  Flatten[Table[ tri2[i, j], {i, -45, 35}, {j, -55, 20}], 1]~Join~
   Flatten[Table[ tri1[i, j], {i, -45, 35}, {j, -55, 20}], 1];
near = Nearest[p2d];
good = Select[triangles, 
   Total[Norm[(near[#, 1][[1]] - #)] & /@ #] < .001 &];
p3d[x_] := SortBy[b, Norm[#[[1 ;; 2]] - x] &][[1]]
sp3d = (p3d /@ #) & /@ good;
Graphics3D[{EdgeForm[None], 
  Polygon /@ (Select[sp3d, Variance[#[[All, 3]]] < .0001 &])}, 
 BoxRatios -> {1, 1, 1}]

At this point I havn't dealt with the boundaries or the overlapping portions of the surface, but It should get you started.

Yes, this is the kick in the arse I needed. I can actually get my bulk triangles at runtime with a little jiggery-pokery, although it won't shed much light on how to perform this procedure more generally though.
I've accepted this answer and will update the question with the full result when I get it. — Crêpo, Jun 06 '16 at 17:11

Joining points into 3D surface

2 Answers2