Solve and design "water flow"

Question

In some strategy game I play, I'll have to change the terrain to make the water flow in some specific way to fulfill my goal. The water flow changes with terrain so if I can change the terrain wisely I can save a lot of money and time. My problem arose here------Whether can I solve this problem with Mathematica?

---

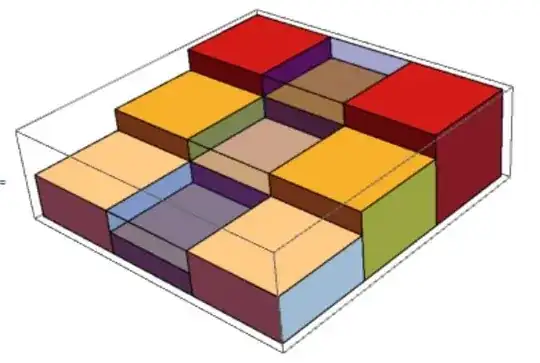
Terrain will be given out with a 2-D matrix, e.g. {{2,3,4},{1,2,3},{2,3,4}} present a terrain that looks like the following figure:

You can visualize a terrain using the following code:

BarChart3D[{{2, 3, 4}, {1, 2, 3}, {2, 3, 4}}, ChartLayout -> "Grid", 
 Method -> {"Canvas" -> None}, ColorFunction -> "TemperatureMap", 
 ChartStyle -> Opacity@.7, ImageSize -> 300, 
 ViewPoint -> {-15, -10, 20}]

---

The water flow in those games follow certain simple rules to make it like real water flow(I admit that it's extremely hard to illustrate it purely by language, so I'll try to demonstrate it with some small examples. :) ):

1. in a normal downward slope, the water keeps the height of 1. (above the terrain)

   So if a terrain can be expressed by {{2,3,4},{1,2,3},{2,3,4}} and the water's origin is at point {2,3}, the water will simply flow down with a constant height 1 along the second row like shown below and the water's height will be like {{0,0,0},{1,1,1},{0,0,0}}.

2. Water flow can create "waterfall".

   So if the terrain takes the form like {{4,5,6},{1,2,5},{4,5,6}} and the origin is at {2,3} the water's height will still be {{0,0,0},{1,1,1},{0,0,0}} and form a "waterfall" between {2,2} and {2,3}. The graphics will be like this:

3. Water will fill the gaps along it's path.

   So if a terrain can be expressed by {{2,3,4,5,6},{1,2,3,2,5},{2,3,4,5,6}} and the water's origin is at point {2,5}, the water will fill the gap at {2,4} and make it with equal height as {2,3}, but at other points on the path, water will keep its own height at 1. the resulting water height will be {{0,0,0,0,0},{1,1,1,2,1},{0,0,0,0,0}}. Check the next figure:

4. water create 'lakes'.

   if there's a gap aside the water flow, the water will rush in the gap as well and create a lake. This concept is hard to describe, so check the following image with terrain: {{6, 6, 6, 6, 6}, {6, 3, 4, 5, 6}, {6, 4, 6, 6, 6}, {5, 4, 3, 2, 1}, {6, 6, 6, 6, 6}} water's origin at {4,5} water: {{0, 0, 0, 0, 0}, {0, 2, 1, 0, 0}, {0, 1, 0, 0, 0}, {1, 1, 1, 1, 1}, {0, 0, 0, 0, 0}}:

---

Well, finally we can get a grip of how the water flow, then we can talk about our problem:

---

1. If the terrain is given, how can we solve out the water's condition?

   TestData:

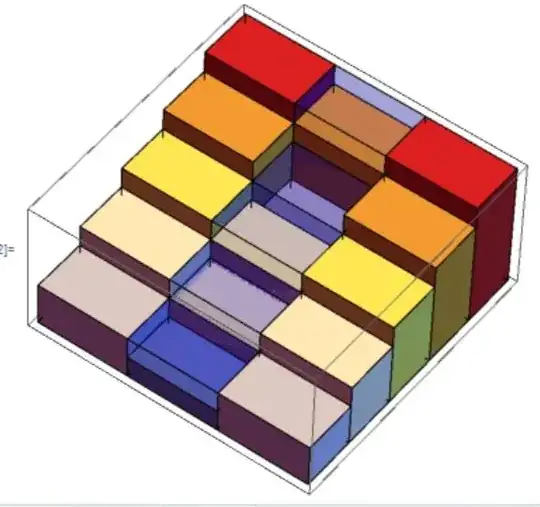
   terrain={{10, 10, 10, 10, 10, 10, 10, 10}, {10, 10, 6, 6, 4, 7, 10, 10}, {10, 10, 7, 10, 5, 10, 10, 10}, {10, 10, 7, 6, 5, 10, 2, 1}, {10, 10, 8, 10, 10, 10, 10, 10}, {10, 9, 8, 6, 4, 5, 2, 1}, {10, 10, 10, 5, 10, 10, 10, 10}, {10, 6, 1, 4, 1, 1, 1, 1}, {10, 6, 6, 3, 2, 1, 1, 1}, {10, 10, 10, 10, 10, 10, 10, 10}}

   origin={6,2}

   The result should be:

   {{0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 3, 3, 5, 2, 0, 0}, {0, 0, 2, 0, 4, 0, 0, 0}, {0, 0, 2, 3, 4, 0, 0, 0}, {0, 0, 1, 0, 0, 0, 0, 0}, {0, 1, 1, 1, 2, 1, 1, 1}, {0, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 4, 1, 1, 1, 1, 1}, {0, 0, 0, 1, 1, 1, 1, 1}, {0, 0, 0, 0, 0, 0, 0, 0}}

---

2. If I marked some points on this map and I need them to be filled with water, how can I minimize the total changes of terrain? (1 change is +1 or -1 on one point of terrain)

---

This problem is quite hard and will really need sometime to read, not to say solve. So really thank everyone who actually read this post and try to solve it. Thanks!!!

---

I actually have one solution for the first problem, but extremely NOT ELEGANT!!! are there any way else to solve the first one?

My code is as follows:

f[terrain_, n_] := 
 Module[{list1 = 
    MorphologicalComponents[UnitStep[n - terrain], 
     CornerNeighbors -> False], 
   list2 = MorphologicalComponents[UnitStep[n + 1 - terrain], 
     CornerNeighbors -> False]}, (1 - 
      Times @@ (Unitize[list1 - #] & /@ 
         Complement[
          Flatten@Select[
             DeleteDuplicates@Thread[Flatten /@ {list1, list2}]~
              DeleteCases~{0, _}~GatherBy~(#[[2]] &)~
              Select~(Length@# > 1 &), 
             MemberQ[list2[[;; , -1]], #[[1, 2]]] && 
               Not@SubsetQ[
                 list1[[;; , -1]], #[[;; , 1]]] &][[;; , ;; , 1]], 
          list1[[;; , -1]]])) (n + 1 - terrain) + terrain]
tm = Fold[f, terrain, Range@Max@terrain - 1];
gra =
  Graph[Flatten[
    Function[{dir, list}, 
      MapIndexed[
       If[#1 == 0, {#2 -> #2 + dir, #2 + dir -> #2}, 
         If[#1 > 0, #2 -> #2 + dir, #2 + dir -> #2]] &, 
       list, {2}]] @@@ {{{1, 0}, Most@tm - Rest@tm}, {{0, 1}, 
       Transpose[Most@Transpose@tm - Rest@Transpose@tm]}}, 3], 
   VertexLabels -> "Name"];
watercal = 
 tm + SparseArray[
   VertexList@
     Reap[DepthFirstScan[gra, {6, 2}, "FrontierEdge" -> Sow]][[2, 
      1]] -> 1, Dimensions@terrain] - terrain

Answer 1

After a while not thinking of this problem, I think I found a better approach, though with similar method.

I modified the terrain a bit so the first row of terrain is set to 0 which symbolize the waterflow's end.

terrain = {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {10, 10, 10, 1, 10, 1, 10, 
    1, 1, 10}, {10, 10, 10, 2, 10, 2, 10, 1, 1, 10}, {10, 7, 10, 10, 
    10, 5, 10, 1, 1, 10}, {10, 4, 5, 5, 10, 4, 10, 1, 2, 10}, {10, 6, 
    10, 6, 10, 6, 5, 4, 3, 10}, {10, 6, 7, 7, 8, 8, 10, 1, 6, 
    10}, {10, 10, 10, 10, 10, 9, 10, 6, 6, 10}, {10, 10, 10, 10, 10, 
    10, 10, 10, 10, 10}};

t = Now;

tab = Block[{hmax = Max@terrain}, 
   terrain + Nest[Block[{mor = MorphologicalComponents[#, CornerNeighbors -> False]},
      # - Unitize[#] (1 - Unitize[mor - mor[[1, 1]]])] &, hmax - terrain, hmax]];

gra = Graph[
   Flatten[Function[{dir, list}, MapIndexed[
       If[#1 == 0, {#2 -> #2 + dir, #2 + dir -> #2}, 
         If[#1 > 0, #2 -> #2 + dir, #2 + dir -> #2]] &, 
       list, {2}]] @@@ {{{1, 0}, Most@tab - Rest@tab}, {{0, 1}, 
       Transpose[Most@Transpose@tab - Rest@Transpose@tab]}}, 3], 
   VertexLabels -> "Name"];

watercal = 
  tab + SparseArray[VertexList@Reap[DepthFirstScan[gra, {8, 6}, "FrontierEdge" -> Sow]][[2, 1]] -> 1,
   Dimensions@terrain] - terrain;

The previously very complex part is reduced to 3 simple lines in tab. And the speed is increased by approximately 2.5 times, though not much, but I believe it would be significant if the terrain matrix is larger.

This is a satisfying answer for me now. Any better method?