Finding area of intersection regions

Question

I want to be able to find the area of the intersection between a hexagon and a slice. I have tried RegionMeasure or Area but I seem to get incorrect answers. RegionMeasure gives length when the intersection is a line, so I switched to Area but sometimes it still gives weird answers, when the intersection happens to be a line.

One reason why I think this might occur is that I build the hexagon using Polygon, but the "slice" is with Disk. Is that the problem? How to I make a region as a slice, so that Area[RegionIntersection[hexagon, slice]] between the two regions will always give $0$ for a line intersection and no intersection, i.e. return a nonzero result only for 2D intersection.

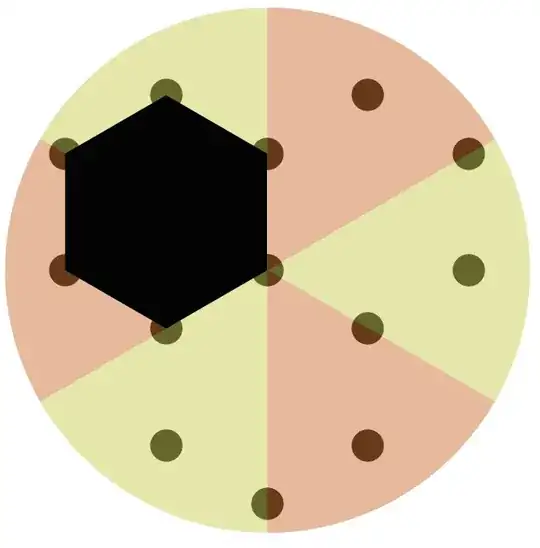
See picture. I want to know the area of intersection of the black hexagon will each of the 6 (colored for visualization) slices below. The answer should be non-zero for the 2 upper left slices, and 0 for every other slice, even though some have "line intersections".

Thanks.

EDIT: The problem is that edges get non-zero measure. Why is the below code giving .7, and not 0?

DiskR = 1.5;
Show[
  Graphics[{Orange, Opacity[0.35], 
  Disk[{0, 0}, DiskR, {Pi/6, 3 Pi/6}]}], 
  Graphics[Polygon[{{0, 0}, {0, .7}, {-1, 1}}]]]

and

Area[
 RegionIntersection[
  Polygon[{{0, 0}, {0, .7}, {-1, 1}}], 
  Disk[{0, 0}, DiskR, {Pi/6, 3 Pi/6}]
 ]
]

This certainly works: Polygon[CirclePoints[{-(Sqrt[3]/2), 1/2}, {1, π/6}, 6]] ~RegionIntersection~ Disk[{0, 0}, 3, {π/2, π/2 + π/3}] // Area — J. M.'s missing motivation, Jun 14 '16 at 15:52
But why does a line give non-zero Area? See my edited question. — Ben S, Jun 14 '16 at 17:05
Please post the code as text. Nobody wants to copy it out manually from the image. — Simon Woods, Jun 14 '16 at 18:08
Sorry, new here. But I see your point. I edited and pasted the code. — Ben S, Jun 14 '16 at 18:15
You didn't include the value of DiskR, but replacing DiskR with 3/2 seems to give something similar to your last figure. However, I can't reproduce your last result: Area[ RegionIntersection[ Polygon[{{0, 0}, {0, .7}, {-1, 1}}], Disk[{0, 0}, 3/2, {Pi/6, 3 Pi/6}] ] ] returns $0$ as you expected, not $0.7$ as you reported (results). I am using MMA 10.4 on Win7-64. What version are you using? — MarcoB, Jun 15 '16 at 17:22
This seems buggy - if you set DiskR= 1.5 then you get the erroneous result from the OP, but if you set DiskR=3/2 (or use Rationalize@DiskR in the call to Disk) then you get the right answer of 0 — Jason B., Jun 16 '16 at 15:40
Yes, when I run DiskR=1.5 (or 2.0 or whatever), I also get 0.7. But using DiskR=3/2 gives 0. If this is a bug, hopeful Mathematica can see this and fix it. I don't know how to report it, though. — Ben S, Jul 06 '16 at 02:44

score 4 · Answer 1 · edited Apr 13 '17 at 12:55

In this case, the intersection between two 2D regions is a 1D region - a line. It makes sense that the functions that are called by RegionMeasure and RegionIntersection might be influenced by roundoff errors associated with using floating point numbers rather than exact numbers.

So a workaround is to convert your expressions to use exact numbers prior to taking the area. I had originally used Rationalize to do this, and it works in this case, but it doesn't always. So we can borrow a function from illian that is a bit more robust

sp = Function[p, SetPrecision[p, Infinity]];    
DiskR = 1.0; 
Area[
 RegionIntersection[sp@Polygon[{{0, 0}, {0, .7}, {-1, 1}}], 
  sp@Disk[{0, 0}, DiskR, {Pi/6, 3 Pi/6}]]]

(* 0 *)

While this behavior is understandable, I'd still say it's a bug

Finding area of intersection regions

1 Answers1

Linked