Speeding iterative computation

Question

I want to get the following iterative sequence

x[0] = 0.9;
T[x_] := Piecewise[{{1 - x, 0 <= x < 1/7}, {(x + 6)/7, 
     1/7 <= x <= 1}}];
a[n_] := n/(n + 5)^5;
b[n_] := (2 n/7 n + 5)^(1/2);
x[n_] := (1 - a[n - 1])* T[x[n - 1]] + 
   a[n - 1]*T[(1 - b[n - 1]) *x[n - 1] + b[n - 1] T[x[n - 1]]];
For[n = 1, n < 50, n++, Print[x[n]]];

But it is taking to much time to execute. In 10 to 15 hours, it reached to the 18 iteration and the required value is still not received, which is 1. I think to reach 1, 20 to 30 iteration must be required.

Is there any other way to reach the answer "1" sooner?

Thanks in advance.

Please use the formatting guide (click {} while typing up your question). As a first suggestion, if you're using loops, you're probably doing something wrong. — Ben Kalziqi, Jun 16 '16 at 18:57
Your code is highly inefficient. For instance, what do you mean by (2 n/7 n + 5)? Is this merely 5 + 2/7 = 37/7? Likewise, do you need the second conditional in your Piecewise? And why define all your functions, e.g., a, when you can merely compute that in x? And by all means replace For with Table and eliminate Print. — David G. Stork, Jun 16 '16 at 19:02
@David G. Stork, (2 n/7 n + 5)is actually 2n/(7n+5). Different function is due to n, if n change, the valve of a, b and then x will be changed with each iteration. — Marwat, Jun 16 '16 at 19:08
Follow @DavidG.Stork 's advice and use Table, or maybe Map. The timing on this function is terrible; moreover, why are you convinced that this even converges to 1 after a finite iterations? — Ben Kalziqi, Jun 16 '16 at 19:25
1 is the fixed point of the function T, and the iterative procedures is the convergence procedure and since it is proved that the procedure is convergent to fixed point — Marwat, Jun 16 '16 at 19:40
um.... 2 n/7 n +5 is 2 n^2 / 7 +5 .. @marwat use some parenthesis. — george2079, Jun 16 '16 at 19:46

score 4 · Accepted Answer · edited Apr 13 '17 at 12:55

4

Use memoization. See here for a description of the memoization in general, and here for its Mathematica implementation. This will avoid having to recalculate all the previous values to determine the next one:

Clear[x, T, a, b]
T[x_] := T[x] = Piecewise[{{1 - x, 0 <= x < 1/7}, {(x + 6)/7, 1/7 <= x <= 1}}]
a[n_] := a[n] = n/(n + 5)^5
b[n_] := b[n] = (2 n/7 n + 5)^(1/2)

x[0] = 0.9;
x[n_] := x[n] = (1 - a[n - 1])*T[x[n - 1]] + 
                  a[n - 1]*T[(1 - b[n - 1])*x[n - 1] + b[n - 1] T[x[n - 1]]]

Table[{i, x[i]}, {i, 0, 50}]

(* Out: {{0, 0.9}, {1, 0.985714}, {2, 0.997831}, {3, 0.999571}, 
         {4, 0.999847}, {5, 0.99991}, {6, 0.999937}, {7, 0.999954}, 
         {8, 0.999965}, {9, 0.999973}, {10, 0.999979}, {11, 0.999984}, {12, 0.999987}, 
         {13, 0.99999}, {14, 0.999992}, {15, 0.999993}, {16, 0.999994}, {17, 0.999995}, 
         {18, 0.999996}, {19, 0.999997}, {20, 0.999997}, {21, 0.999998}, 
         {22, 0.999998}, {23, 0.999998}, {24, 0.999998}, {25, 0.999999}, {26, 0.999999}, 
         {27, 0.999999}, {28, 0.999999}, {29, 0.999999}, {30, 0.999999}, {31, 0.999999}, 
         {32, 0.999999}, {33, 0.999999}, {34, 1.}, {35, 1.}, {36, 1.}, {37, 1.}, {38, 1.}, 
         {39, 1.}, {40, 1.}, {41, 1.}, {42, 1.}, {43, 1.}, {44, 1.}, {45, 1.}, {46, 1.}, 
         {47, 1.}, {48, 1.}, {49, 1.}, {50, 1.}}
*)

Also, avoid loops (For, Do), but rather use vector constructs (e.g. Table, Map). The Table above now calculates almost instantaneously.

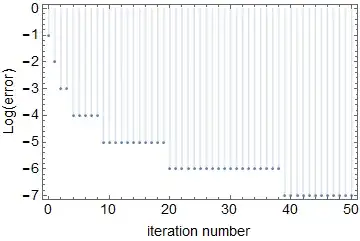
If you are interested in how far from exactly $1$ the value of $x(i)$ is for a certainly value of $i$, then you may resort to arbitrary precision calculations, after changing the precision of your starting point x[0]. For instance, using 20-digit precision calculations:

x[0] = 0.9`20;

DiscretePlot[
 Round@Log10[Abs[x[i] - 1]], {i, 0, 50},
 Frame -> True, LabelStyle -> {Black, 14},
 FrameLabel -> {"iteration number", "Log(error)"}
]

Mathematica graphics

edited Apr 13 '17 at 12:55

Community

1

answered Jun 16 '16 at 19:31

MarcoB

67,153
18
91
189

1

Thanks a lot @MarcoB. It works very very beautifully – Marwat Jun 16 '16 at 19:43
Sir Is the value of 1 is exact? – Marwat Jun 16 '16 at 19:52
@Marwat It is indistinguishable from $1$ at the precision at which the claculation was carried out, which happens to be machine precision because you specified 0.9 as a starting point. If you want exact results, use x[0] = 9/10; if you want higher precision numerical results, say e.g. to 20 digits of precision, then use x[0] = 0.9`20. – MarcoB Jun 16 '16 at 20:00
@Marwat See also the addition to my answer above – MarcoB Jun 16 '16 at 20:06
Thanks a lot. Now I understand. I think 1. is not exact but 1 is exact. Now Sir please tell me about the plotting of graph. Let us call the about function [x_n], the M function. And let us suppose there is one another function say K function, for example K function is x[n_] := (1 - a[n - 1])* T[x[n - 1]] + a[n - 1]T[(1 - b[n - 1]) x[n - 1] + b[n - 1] T[x[n - 1]]]. Now we need to draw the graphs of both M and K function to compare the convergence. Please help..... – Marwat Jun 17 '16 at 12:03
@Marwat Since this second part of your problem is not really related to your original question, it would be best for you to start a new, different question on this site, rather than continuing the discussion in comments. "Moving target" questions are discouraged. – MarcoB Jun 17 '16 at 13:37
okey Sir thanks a lot for so much cooperation – Marwat Jun 17 '16 at 18:52
What is meant by Log(error) by definition? – Marwat Jun 19 '16 at 10:45
@Marwat I'm not using that rigorously. I just mean to show the order of magnitude of the difference between the value of the recursion after a certain number of iterations and $1$, the convergence value. So a value of -6 indicates that the value of the recursion after a certain number of steps is only $10^{-6}$ units away from $1$. It's not properly an error, but I'd didn't have a better name for it at the time. – MarcoB Jun 19 '16 at 14:27
@Marco_B thanks for explanation. So what can be the better name for it? – Marwat Jun 20 '16 at 19:23
@Marwat "Log (distance from convergence)" perhaps? – MarcoB Jun 20 '16 at 19:57
@Marwat You are very welcome. If you think that my answer appropriately addressed your problem, you could consider formally accepting it by clicking on the grey check mark next to it. – MarcoB Jun 23 '16 at 00:24
What you mean by "you could consider formally accepting it by clicking on the grey check mark next to it"? it is not clear to me? – Marwat Jun 24 '16 at 10:31

Speeding iterative computation

1 Answers1