Data Fitting problem

Question

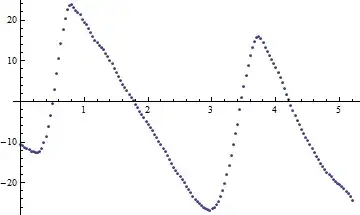
I'm having this kind of data, and I know what possibly the equation is, i suspect this has a sine equation but the plot not really seems sinusoid. so what possibly the equation is so i can do the nonlinearmodelfit?

Is this all the data you have? With so many features in your data and no firm idea of a model, I am not sure that the results of any fitting will be very meaningful. — MarcoB, Jun 17 '16 at 14:20
You certainly could look into Fourier[], but I'd be wary of proposing a solution without knowledge of the data's provenance. — J. M.'s missing motivation, Jun 17 '16 at 14:23
stuff here might be useful http://mathematica.stackexchange.com/q/38293/2079. When you say "I know what possibly the equation is", why don't you share what you know? — george2079, Jun 17 '16 at 16:08
As a follow-up to @MarcoB 's comment: What is it that you need? Do you need just to succinctly describe the data? Do you need to predict past the value 5.2 ? Do you need to reproduce the curve in some other program? If it's just reproducing the underlying curve, then maybe connecting the dots is all you need (i.e., interpolation). Will there be additional samples that you'll need to compare against? In summary, your objective is currently a bit too vague to give specific advice. — JimB, Jun 17 '16 at 22:47

score 6 · Answer 1 · edited Apr 13 '17 at 12:55

I extracted the data from the image using "Recovering data points from an image".

ListPlot[extractedData, PlotRange -> All, PlotTheme -> "Detailed"]

Then I applied NonLinearModelFit over that data for a list of sinusoids (and a constant):

baseFuncs = Prepend[Table[Sin[k x Pi/5.25], {k, 1, 30}], 1];

vars = Array[a, Length[baseFuncs]];

nf = NonlinearModelFit[extractedData, vars.baseFuncs, vars, x]

Here is the found function:

nf["Function"][x]

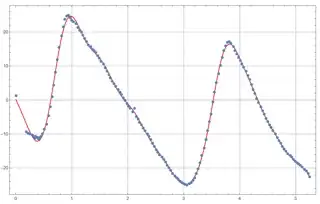
The found fit looks pretty good:

gr1 = Plot[
   nf["Function"][x], {x, Min[extractedData[[All, 1]]], 
    Max[extractedData[[All, 1]]]}, PlotStyle -> Red, PlotRange -> All,
    PlotTheme -> "Detailed"];
gr2 = ListPlot[extractedData];
Show[{gr1, gr2}

Update

In relation to a comment by @JimBaldwin let us look into the predictions/extrapolations using the found fit:

Note that with the basis functions defined as:

baseFuncs = Prepend[Table[Sin[k x (Pi/2)/5.25], {k, 1, 30}], 1];

we get a good fit within the range of the data:

but not very meaningful results in larger ranges:

Data Fitting problem

1 Answers1

Update