5

I want to solve Laplace equation in 2D with $x$ and $y$ coordinates with the boundary conditions $V(0,y)=-180$; $V(x,0)=50x-180$; $V(x,6)=50x-180$; $V(453.595-\sqrt{450.05^2 - (y - 3)^2},y)=0$ The problem is the fourth boundary is the segment of a circle. I want to find $V(x,y)$ within the boundary.

Is this problem solvable using Mathematica? anyone with any idea? I have been struggling with this problem for my research work could find only approximate analytical solution and want to compare the results if solvable by Mathematica.

enter image description here

Young
  • 7,495
  • 1
  • 20
  • 45
Ajib Paudel
  • 109
  • 6
  • 4
    Have a look in the documentation: NDSolve is what you are looking for. If you need help with something concret why don't you post the code you have. – user21 Jun 25 '16 at 04:43

1 Answers1

11

Setup The region to solve the PDEs

Clear["Global`*"]

xMax = 453.595 - Sqrt[450.05^2 - 3^2];
regA = Rectangle[{0, 0}, {xMax, 6}];
regB = ImplicitRegion[{453.595 - Sqrt[450.05^2 - (y - 3)^2] - x < 0}, 
       {{x, 0, xMax}, {y, 0, 6}}];
reg = RegionDifference[regA, regB];

RegionPlot[reg, AspectRatio -> 1/10]

enter image description here

Solve the PDEs using NDSolve

solV = NDSolveValue[{D[u[x, y], x, x] + D[u[x, y], y, y] == 0,
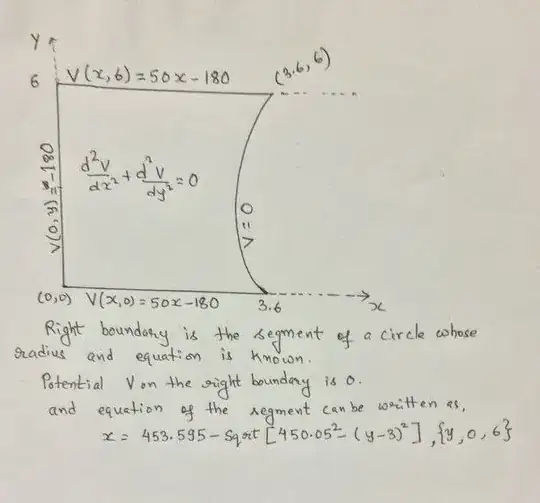
   DirichletCondition[u[x, y] == 0, 453.595 - Sqrt[450.05^2 - (y - 3)^2] == x],
   DirichletCondition[u[x, y] == -180, x == 0],
   DirichletCondition[u[x, y] == 50 x - 180, y == 0],
   DirichletCondition[u[x, y] == 50 x - 180, y == 6]}, 
  u, {x, y} \[Element] reg]

DensityPlot[solV[x, y], {x, y} \[Element] reg, Mesh -> None, 
 ColorFunction -> "Rainbow", PlotRange -> All, 
 PlotLegends -> Automatic, AspectRatio -> 1/10]

Potential Map:

enter image description here

Check out other examples on Mathematica SE

Electric Field Vectors:

eleField[x_, y_] = -Grad[solV[x, y], {x, y}];

Show[
 DensityPlot[solV[x, y], {x, y} \[Element] reg, Mesh -> None, 
  ColorFunction -> "Rainbow", PlotRange -> All, 
  PlotLegends -> Automatic, AspectRatio -> 1/10, ImageSize -> Full],
 VectorPlot[eleField[x, y], {x, y} \[Element] reg, VectorPoints -> 5, 
  VectorStyle -> Gray, VectorScale -> Small, AspectRatio -> 1/10]
 ]

enter image description here

Community
  • 1
Young
  • 7,495
  • 1
  • 20
  • 45
  • Yes, this code solves the Laplace equation for any geometry. Also, the example for finding Electric field is helpful. I appreciate this. Thanks. – Ajib Paudel Jun 27 '16 at 03:46