First of all, I want to say that I'm quite new to Mathematica. I searched a lot on this site to learn how to solve my problem, which this is the problem of my life! I want to minimize a function. It is a chemical problem regarding a famous equation of state called the Peng-Robinson equation of state.
Perhaps I'm did something wrong when defining my function or there is an error in the numerical minimization, but I can't understand where where the problem is. So I'll appreciate any suggestions,
(*Preparing variables*)
T = {100};
tc = {126.1, 190.6};
pc = {33.94, 46.04};(*MPa*)
ω = {0.040, 0.011};
R = 83.14472;
P = 4.119;
x1 = 0.5;
x2 = 1 - x1;
y1 = 0.958;
y2 = 1 - 0.958;
k12 = 0;
lunghezza = Length[T];
m12 = -0.26992*ω^2 + 1.54226*ω + 0.37464;
a12vet = Table[
0.45724*(R*tc[[j]])^2/
pc[[j]]*(1 + m12[[j]] (1 - (T[[i]]/tc[[j]])^(1/2)))^2, {i,
lunghezza}, {j, {1, 2}}];
b12 = 0.0778*R*tc/pc;
b1 = b12[[1]];
b2 = b12[[2]];
a1 = a12vet[[All, 1]];
a2 = a12vet[[All, 2]];
a12 = (a1*a2)^(1/2) (1 - k12);
a = (x1)^2*a1 + 2*x1*x2*a12 + (x2)^2*a2;
b = x1*b1 + x2*b2;
(*Function to minimize*)
funcion[yy1_, PP_] :=
Module[{yy2, A11, A22, B1, B2, A12, BVap, AVap, ALiq, BLiq},
yy2 = 1 - yy1;
A11 = (a1*PP)/(R^2*T^2);
A22 = (a2*PP)/(R^2*T^2);
B1 = (b1*PP)/(R*T);
B2 = (b2*PP)/(R*T);
A12 = Sqrt[A11*A22];
BVap = yy1*B1 + yy2*B2;
AVap = yy1^2 A11 + 2 yy1 yy2 A12 + yy2^2 A22;
ALiq = x1^2 A11 + 2*(x1*x2)* A12 + x2^2 A22;
BLiq = x1*B1 + x2*B2;
solzv =
NSolve[Z - 1/(1 - BVap/Z) +
AVap/BVap*BVap/Z/(1 + 2 *BVap/Z - (BVap/Z)^2) == 0, Z];
solsv = Z /. {solzv[[1]], solzv[[3]]};
solv = solsv[[1]];
solzl =
NSolve[Z - 1/(1 - BLiq/Z) +
ALiq/BLiq*BLiq/Z/(1 + 2 *BLiq/Z - (BLiq/Z)^2) == 0, Z];
solsl = Z /. {solzl[[1]], solzl[[3]]};
soll = solsl[[2]];
Subscript[lnϕ, 1 v] =
B1/BVap (solv - 1) - Log[solv - BVap] -
AVap/(BVap Sqrt[8])
Log[(solv + (1 + Sqrt[2]) BVap)/(
solv + (1 - Sqrt[2]) BVap)] ((2 (yy1 A11 + yy2 A12))/AVap - B1/
BVap);
Subscript[lnϕ, 2 v] =
B2/BVap (solv - 1) - Log[solv - BVap] -
AVap/(BVap Sqrt[8])
Log[(solv + (1 + Sqrt[2]) BVap)/(
solv + (1 - Sqrt[2]) BVap)] ((2 (yy1 A12 + yy2 A22))/AVap - B2/
BVap);
Subscript[ϕ, 1 v] = Exp[Subscript[lnϕ, 1 v]];
Subscript[ϕ, 2 v] = Exp[Subscript[lnϕ, 2 v]];
Subscript[lnϕ, 1 l] =
B1/BLiq (soll - 1) - Log[soll - BLiq] -
ALiq/(BLiq Sqrt[8])
Log[(soll + (1 + Sqrt[2]) BLiq)/(
soll + (1 - Sqrt[2]) BLiq)] ((2 (x1 A11 + x2 A12))/ALiq - B1/
BLiq);
Subscript[lnϕ, 2 l] =
B2/BLiq (soll - 1) - Log[soll - BLiq] -
ALiq/(BLiq Sqrt[8])
Log[(soll + (1 + Sqrt[2]) BLiq)/(
soll + (1 - Sqrt[2]) BLiq)] ((2 (x1 A12 + x2 A22))/ALiq - B2/
BLiq);
Subscript[ϕ, 1 l] = Exp[Subscript[lnϕ, 1 l]];
Subscript[ϕ, 2 l] = Exp[Subscript[lnϕ, 2 l]];
Abs[(Subscript[ϕ, 1 v] - Subscript[ϕ,
1 l]) + (Subscript[ϕ, 2 v] - Subscript[ϕ, 2 l])]
]
(*Minimization*)
(*Does my function pass all variables?*)
funcion[0.9186212148724066`, 4]
(* {0.171251} *)
NMinimize[{funcion[yy1, PP], 0 < yy1 < 1 && 0 < PP < 10}, {yy1, PP}]

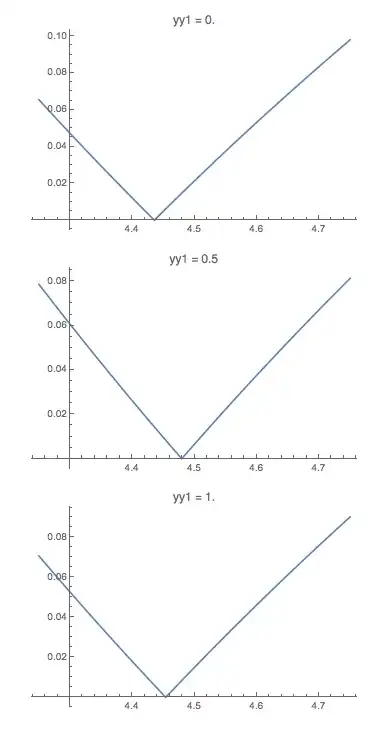
NSolve(2) state clearly what the problem is. – Szabolcs Jun 27 '16 at 09:36NMinimize[{funcion[yy1, PP][[1]], 0 < yy1 < 1 && 0 < PP < 10}, {yy1, PP}]– vapor Jun 27 '16 at 09:40