Cluster a signal into areas of equal intensity

Question

Introduction

I have a greyscale photograph that I want to partition into areas of equal intensity. This means, that the integral over each partition should be (roughly) equal. There is no unique solution to this problem, but although I have some ideas on how to implement it, I am looking for any effective solutions for bitmap input.

1D-example

Let f be my signal, and g it's strictly positive, "padded" version:

f[x_] = 0.2 Cos[5 x] + Sin[x];
const = First[Minimize[f[x], {x}]];
g[x_] := 0.1 + f[x] - const;
G[x_] = Integrate[g[s], {s, 0, x}];

My signal is now of total intensity

max = G[4 π];

and I can divide my y-axis into equal segments

k = 20;
sols = Table[FindRoot[G[x] - y == 0, {x, y}], {y, Range[0, max, max/(k - 1)]}];

and by intersecting these segments with my integral curve, I can project to the x-axis and get my desired intervals:

Show[
 {
  Plot[{g[x], G[x]}, {x, 0, 4 π}, PlotStyle -> {{Thick, Green}, Red}],
  Graphics[Point[{#, G[#]}] & /@ (x /. sols)],
  Graphics[Line[{{0, G[#]}, {#, G[#]}, {#, 0}} & /@ (x /. sols)]]
  }
 ]

Which gives me

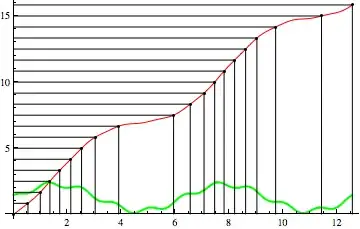
Mathematica graphics

2D-case

I can imagine that this method generalises to 2D, but it is unclear how to implement it. Also, a big penalty comes from attempts at interpolating the image.

Another idea is to use Sasha's solution for sampling a probability distribution (in my case, the image itself):

RandomVariate from 2-dimensional probability distribution

Thereafter one can generate the Voronoi-diagram for the sample. However, I have been unable to create a feasible solution using this method as well.

It seems to me, that this is a problem better approached by a combination of image processing algorithms. After all, all my input is, is a bitmap. However, after researching this, I could not find a previous description of the problem (or a solution for that matter) in any of the image-processing communities.

Questions

Does this problem have an actual name in the community already?
Can I find an efficient way of clustering a signal, preferably working on the discrete data, into regions of similar intensity?
(Bonus points) Can I generate grids with nice combinatorics? There is a nice Z-combinatorics for the 1D-example of course. Although a Z^2 grid for the 2D-case is too much to ask, perhaps there is a way to get a Quadtree-looking grid?

This question seems a better fit for the signal processing site — Dr. belisarius, Oct 12 '12 at 12:20
I checked it out, and though I partly agree, I just named this a "signal" in order to open up the question to more than image processing specialists. In addition, I am specifically looking for a Mathematica solution. — kejace, Oct 12 '12 at 12:23
But you need an algorithm first ... I think. Anyway, perhaps someone can come up with something here, mine was only a suggestion — Dr. belisarius, Oct 12 '12 at 12:26
related http://stats.stackexchange.com/questions/8744/clustering-procedure-where-each-cluster-has-an-equal-number-of-points — Dr. belisarius, Oct 12 '12 at 13:26
You could also try quadtree segmentation - the Wolfram Demo is pretty fast http://demonstrations.wolfram.com/QuadTreeImageDecomposition/ — dr.blochwave, Feb 08 '16 at 07:42

Dr. belisarius · Answer 1 · 2016-02-08T05:35:15.927

The following seems to work at least for small grayscale images and a few points. My current computing power doesn't allow me to test it for larger examples. As this question was posed more than three years ago I decided to post this, despite the fact that I don't know how it scales.

It makes a Voronoi partition and minimizes the Variance of the region intensities.

voronoi[pts_] :=
 (* BoundedDiagram fails too often, so I'm using Vitaliy's nice 
              http://mathematica.stackexchange.com/a/39828/193*)
 Binarize@ImageResize[ImageCrop[
    ListDensityPlot[Append[#, 0] & /@ pts, InterpolationOrder -> 0, 
     BoundaryStyle -> Black, Frame -> False, ColorFunction -> (White &)]], id]

calcIntensities[{i_Image, voronoi_Image}] := 
 (*probably can be made faster by using the Polygon from Voronoi instead of
   ComponentMeasurements *)
 ImageMeasurements[#, "TotalIntensity"] & /@ (ImageMultiply[i, mage@#] & /@ 
     (ComponentMeasurements[voronoi, "Mask", CornerNeighbors -> False][[All, 2]]))

obj[i_Image, pts_?(VectorQ[#, VectorQ[#, NumericQ] &] &)] := 
                 Variance@calcIntensities[{i, voronoi[pts]}]

Usage:

ed = ExampleData /@ ExampleData["AerialImage"][[1 ;; 5]];
imgs = ColorConvert[ImageResize[#, 100], "Grayscale"] & /@ ed;
(*Three segments*)
pts = Array[p, {3, 2}];
id = First@ImageDimensions[imgs[[1]]];
nm = NMinimize[{obj[#, pts], And @@ Thread[1 < Flatten@pts < id]}, 
               Flatten@pts, Method -> "NelderMead"] & /@ imgs;

Result:

Mathematica graphics

Result table code

TableForm[{#[[1]], ImageMultiply@@#, Sequence@@{#, Variance@#} &@calcIntensities[#]} &/@ 
          Transpose[{imgs, voronoi /@ (pts /. nm[[All, 2]])}], 
          TableHeadings -> {{}, {"Original", "Segmentation", 
                                 "Intensity Values", "Variance"}}]

Edit

The following incarnation is 50% faster:

voronoi[pts_] := Module[{g},
  g = ListDensityPlot[Append[#, 0] & /@ pts, InterpolationOrder -> 0, 
                      Frame -> False, PlotRange -> {{0, id}, {0, id}}];
  (Graphics[{FaceForm[White], Polygon@#}, Background -> Black, 
      PlotRange -> {{1, id - 1}, {1, id - 1}}, PlotRangePadding -> 0, 
      ImageSize -> id] & /@ 
    Cases[Cases[g, _GraphicsComplex] // Normal, Polygon[l_, ___] :> l, Infinity])]

calcIntensities[{i_Image, voronoi_}] := 
 ImageMeasurements[#, "TotalIntensity"] & /@ (ImageMultiply[i, Image@#] & /@ voronoi)

obj[i_Image, pts_?(VectorQ[#, VectorQ[#, NumericQ] &] &)] := 
 Variance@calcIntensities[{i, voronoi[pts]}]

Usage:

i = ColorConvert[ImageResize[ExampleData[{"TestImage", "Mandrill"}], 100], "Grayscale"];
pts = Array[p, {3, 2}];
id = First@ImageDimensions@i;
Timing[nm = NMinimize[{obj[i, pts], And @@ Thread[1 < Flatten@pts < id]}, 
            Flatten@pts, Method -> "NelderMead"]]

(ImageMultiply[i, #] & /@ voronoi[pts /. nm[[2]]])
ImageMeasurements[#, "TotalIntensity"] & /@ (ImageMultiply[i, #] & /@ voronoi[pts /. nm[[2]]])

Mathematica graphics

Fold[ImageAdd@## &, (ImageMultiply[i, #] & /@ voronoi[pts /. nm[[2]]])]

Mathematica graphics

Just for the record, here is 4-partitioned mandrill image. The performance is horrific:

Mathematica graphics

Anton Antonov · Answer 2 · 2016-02-08T14:28:14.333

The code in this answer implements a 2D version of the approach in the question. It is fairly fast but does not have great precision. The achieved precision might be seen as good enough.

Get image data (as in the set up of the answer by Dr. belisarius):

ed = ExampleData /@ ExampleData["AerialImage"][[1 ;; 5]];
imgs = ColorConvert[ImageResize[#, 500], "Grayscale"] & /@ ed;
imgArr = Reverse[imgs[[1]] // ImageData];

The original approach can be re-written to use accumulated sums intestead of integration. The following function does that.

GetSplitCoords[vec_?VectorQ, args___] := GetSplitCoords[{vec}, args];
GetSplitCoords[vecs : {_?VectorQ ..}, qs_: Range[0, 1, 0.1]] :=
  Block[{qvals, accVec = Total /@ Accumulate[Transpose[vecs]]},
   qvals = Rescale[qs, {Min[qs], Max[qs]}, {0, Max[accVec]}];
   Map[Block[{t = Abs[accVec - #]}, Position[t, Min[t]][[1, 1]]] &, 
    qvals]
   ];

Here are partitioning coordinates:

qs = Range[0, 1, 0.2];

Find the separation curves in $X$ and $Y$ direction in an alternating manner:

rowCoords = 
  Transpose@
   MapIndexed[Thread[{#2[[1]], GetSplitCoords[#1, qs]}] &, 
    Transpose[imgArr]];
colCoords = 
  Transpose@
   MapIndexed[Thread[{GetSplitCoords[#1, qs], #2[[1]]}] &, imgArr];

Instead of using the accumulated sum of a single vector to find a splitting point we can use the accumulated sum of several vectors:

pStep = 20; offset = Floor[(pStep - 1)/2];
rowCoords = Transpose@MapIndexed[Thread[{#2[[1]], GetSplitCoords[#1, qs]}] &,
    Join[Transpose[imgArr][[1 ;; offset]], 
     Partition[Transpose[imgArr], pStep, 1], 
     Transpose[imgArr][[-(pStep - offset - 1) ;; -1]]]];
colCoords = 
  Transpose@MapIndexed[Thread[{GetSplitCoords[#1, qs], #2[[1]]}] &, 
    Join[imgArr[[1 ;; offset]], Partition[imgArr, pStep, 1], 
     imgArr[[-(pStep - offset - 1) ;; -1]]]];

Plot the found parition lines over the image:

Show[{
  Graphics[Raster[imgArr]],
  ListLinePlot[colCoords, PlotStyle -> Yellow],
  ListLinePlot[rowCoords, PlotStyle -> Yellow]}, Frame -> True]

At this point we want to extract the segments of the image between the grid lines.

Find the $X$ segments:

xSegments =
  Table[
   Thread[Thread[{k, 
       Range[rowCoords[[i, k]][[2]], rowCoords[[i + 1, k]][[2]]]}] -> 
     imgArr[[k, rowCoords[[i, k]][[2]] ;; rowCoords[[i + 1, k]][[2]]]]],
   {i, 1, Length[rowCoords] - 1}, {k, 1, Length[rowCoords[[i]]]}];
xSegments = SparseArray[Flatten[#], Dimensions[imgArr]] & /@ xSegments;

Find the $Y$ segments:

ySegments =
  Table[
   Thread[Thread[{Range[colCoords[[i, k]][[1]], colCoords[[i + 1, k]][[1]]], 
       k}] -> imgArr[[colCoords[[i, k]][[1]] ;; colCoords[[i + 1, k]][[1]], 
      k]]],
   {i, 1, Length[colCoords] - 1}, {k, 1, Length[colCoords[[i]]]}];
ySegments = SparseArray[Flatten[#], Dimensions[imgArr]] & /@ ySegments;

Lets plot the $X$ segments:

Graphics[Raster[#]] & /@ xSegments

Precision of the $X$ segments:

Map[Total[#, 2] &, xSegments]

(* {16752.8, 18665., 23587., 22058.2, 32367.5} *)

Precision of the $Y$ segments:

Map[Total[#, 2] &, ySegments]

(* {31279.3, 24490., 20210.1, 22910.4, 14562.5} *)

Make filtering matrices to extract the grid segments:

xSegments01 = 
  Map[Function[{sm}, 
    SparseArray[Thread[Most[ArrayRules[sm]][[All, 1]] -> 1], 
     Dimensions[sm]]], xSegments];
ySegments01 = 
  Map[Function[{sm}, 
    SparseArray[Thread[Most[ArrayRules[sm]][[All, 1]] -> 1], 
     Dimensions[sm]]], ySegments];
filterMats = 
  Flatten[Table[s1*s2, {s1, xSegments01}, {s2, ySegments01}], 1];

Extract the segments:

segments = Map[imgArr*# &, filterMats];

Precision of the intesity separation over the segments:

t = Map[Total[#, 2] &, segments];
ListPlot[Sort[t/Median[t]], GridLines -> {None, {1}}]

We can see the precision is not that great. With some images I get much better precision with some worse.

Here is what we get with a single vector accumulated sums (the obtained grid can be pretty jagged):

The

Cluster a signal into areas of equal intensity

2 Answers2

Linked