I am solving nonlinear ODE + integration groups using NDSolve of mma and ode45 of matlab. At last, I found that they give different results, even after I added RungeKutta method, interpolationorder, changed the value of precisiongoal, and accuracygoal of NDSolve. Do the different answer origin from numerical error, or the wrong coding?
The equations I want to solve are as below. I want to solve v(z),qr(z) and qi(z) and plot v(z0)&b(z0)&qi(z0) v.s.z0, where b=Sqrt(1/qr)/k0, z=z0*k0. The initial conditions are, v(0)=1,b0=100,qi(0)=0, N=100.
MMA codes and results (solve v(z),qr(z),qi(z); b=1/qr^2; plot v(z0), b(z0), qi(z0) v.s. z0=z/k0)
Clear["`*"]
np = 8.;
\[Beta] = 9.5*10^-7;
k0 = 2 Pi;
I0I14 = 1.;
b0 = 100.;
z0max = 100000.;
zmax = z0max*k0;
qr0 = 1/(k0*b0)^2;
ek = 6*10^-5*I0I14* v^2*Exp[-2*qr*rho^2];
ep = 1.8*10^-4*1*I0I14^8*(v^2*Exp[-2*qr*rho^2])^8;
er = 1. + ek + ep;
ei = 9.5*10^-7*I0I14^7* (v^2*Exp[-2*qr*rho^2])^7;
{coreA[v_, qr_, qi_, rho_], coreB[v_, qr_, qi_, rho_]} =
Exp[-qr rho^2] rho RotationMatrix[-qi rho^2].{ei, 1 - er};
int[core_, v_, qr_, qi_?NumericQ] :=
v NIntegrate[core[v, qr, qi, rho], {rho, 0, Infinity}, MaxRecursion -> 40]
intD = \[Beta]/np*I0I14^7;
eqn = With[{v = v@z, qr = qr@z, qi = qi@z},
With[{intA = int[coreA, v, qr, qi], intB = int[coreB, v, qr, qi]},
{D[v, z] == -intA qr - intD v^(2*np - 1),
D[qr, z] == -2 intA qr^2/v - intD qr v^(2*np - 2),
D[qi, z] == -3 intA qi qr/v + intB qr^2/v - intD qi v^(2*np - 2)
}]];
bc = {v[0] == 1., qr[0] == qr0, qi[0] == 0.};
sol = NDSolve[{eqn, bc}, {v, qr, qi}, {z, 0., zmax}, InterpolationOrder -> All]
LogLinearPlot[v[z*k0] /. sol[[2]] // Evaluate, {z, z0min, z0max}]
LogLinearPlot[{Sqrt[1/qr[z*k0]]/k0} /. sol[[2]] // Evaluate, {z, z0min, z0max}]
LogLinearPlot[{qi[z*k0]} /. sol[[2]] // Evaluate, {z, z0min, z0max}]
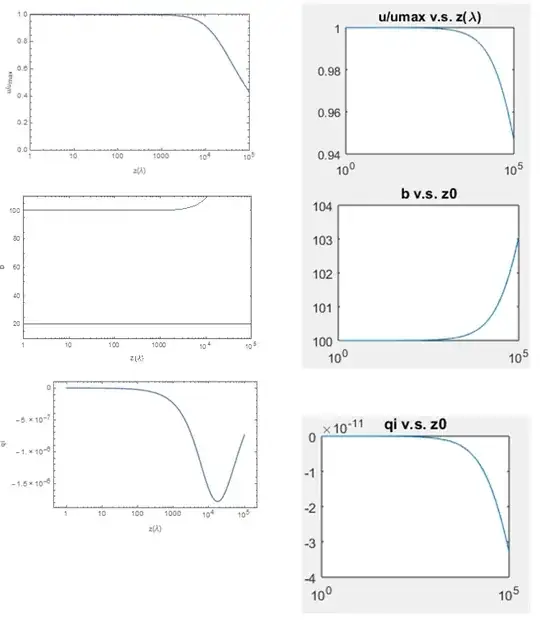
Matlab codes and results, y(1)=v, y(2)=qr, y(3)=qi:
clear all
k0 = 2 * pi; nu_0 = 1;
b0 = 100;
b_0 = b0 * k0;
qr_0 = 1/b_0^2; % initial qr
qi_0 = 0;
options = odeset('RelTol',1e-3,'AbsTol',[1e-4 1e-4 1e-4]);
ts0 = 0;
tf0 = 1E5;
ts = round(0 * k0);
tf = round(tf0 * k0);
nsteps = 1E5;
step = (tf - ts) / nsteps;
tspan = linspace(ts, tf, nsteps);
T = zeros(nsteps,1);
F = zeros(nsteps,3);
warning('OFF','MATLAB:integral:MinStepSize');
[T,F] = ode45(@test_fun,tspan,y0,options);
%------------Plot--------------%
z0 = T / k0;
nu = F(:,1);
qr = F(:, 2);
qi = F(:, 3);
b0 = 1./(F(:,2)).^0.5 / k0;
plot(z0, nu);
set(gca,'XScale','log')
plot (z0, b0);
set(gca,'XScale','log')
plot (z0, qi);
set(gca,'XScale','log')
-----------function------------
function dy=test_fun(x,y)
I14 = 1;
beta = 9.5 * 10^(-7);
np = 8;
ee = @(r)(I14 * y(1)^2 * exp(-2 * y(2) * r.^2));
ek = @(r) (6 * 10^(-5) * ee(r));
ep = @(r) (1.8 * 10^(-4) * 1 * ee(r).^8);
er = @(r) (1 + ek(r) + ep(r));
ei = @(r) (9.5 * 10^(-7) * ee(r).^7);
% A, B, D
A_func = @(r)(exp(-y(2) * r.^2).* ((1 - er(r)).* sin(y(1) * r.^2 * pi/180) + ei(r).* cos(y(3)* r.^2 * pi/180)).* r);
A = y(1) * integral(A_func, 0, Inf);
B_func = @(r)(exp(-y(2) * r.^2).* ((1 - er(r)).* cos(y(1) * r.^2 * pi/180) - ei(r).* sin(y(3) * r.^2 * pi/180)).* r);
B = y(1) *integral(B_func, 0, Inf);
D = beta * I14^7 / np;
dy = zeros(3,1);
dy(1) = -A * y(2) - D * y(1)^(2 * np - 1);
dy(2) = -2 * A * y(2)^2 / y(1) - D * y(2) * y(1)^(2 * np -2);
dy(3) = -3 * A * y(2) * y(3) / y(1) + B * y(2)^2 / y(1) - D * y(3) * y(1)^(2 * np - 2);
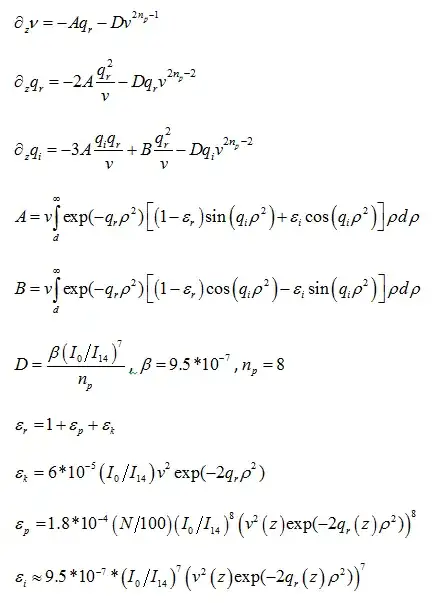
NDSolve, too, see the tutorialtutorial/NDSolveExplicitRungeKutta. If still get different results, then the method ofNDSolveisn't the problem. – xzczd Jul 02 '16 at 07:01WorkingPrecision->16inNDSolveandNIntegrate? (Remember to make all the parameters exact e.g.1.6should be write as16/10.) BTW, you seem to believe the issue is on Mathematica side, any reason? – xzczd Jul 03 '16 at 05:21WorkingPrecision->16and make the parameter exact. One reason that I doubt on the Mathematica side is that the ressults will be different when I change theworkingprecision,precisiongoal; another is that mma is more complicated than matlab. – sixpenny Jul 03 '16 at 08:53WorkingPrecision->16doesn't make a difference, it's sufficient to think this is not a precision issue. As toPrecisionGoalyou may want to read this post. I don't think "mma is more complicated than matlab" is a good reason. Though I'm not that familiar with matlab, the linewarning('OFF','MATLAB:integral:MinStepSize');suggests matlab (also) has trouble in calculating the integration, right? Also, while ode45 is variable step algorithm, you seem to manually fix the step in ode45 bytspan = linspace(ts, tf, nsteps);, why? – xzczd Jul 03 '16 at 11:12