One way to try to "visualize" a 4D object is to take 3D hyperplane sections. A hyperplane is determined by a normal vector and a point. By varying each, one might construct a series that is informative. (One needs to have a good idea of what one is after, since there are many degrees of freedom and understanding the output is difficult.) I'll show how to do one or two sections.
The basic idea is to find a point preferably in the region so that the section will be nonempty in a neighborhood you can find. Pick a normal and complete it to an orthonormal basis we'll call coordsys. Basically, X == coordsys.Z + point, where X == {x11, x12, x21, x22} and Z = {z1, z2, z3, z4} are new coordinates. The hyperplane corresponds to the equation z1 == 0 or the parametrization coordsys.{0, z2, z3, z4} + point.
The OP's regiondescriptor emits error when the eigenvalues are complex. It's not clear whether such a point should be in the region or not. I rewrote the code so that they are excluded, but it can be adjusted to other criteria.
regiondescriptor[x11_, x12_, x21_, x22_] :=
Tr[{{0.09`, 0}, {0, 7}}.{{x11, x12}, {x21, x22}}] >= 1 &&
Tr[{{7, 0}, {0, 0.09`}}.{{x11, x12}, {x21, x22}}] >= 1 &&
Tr[{{1.05`, -0.95`}, {-0.95`, 1.05`}}.{{x11, x12}, {x21, x22}}] >= 1 &&
Tr[{{1.05`, 0.95`}, {0.95`, 1.05`}}.{{x11, x12}, {x21, x22}}] >= 1 &&
With[{eigs = Eigenvalues[{{x11, x12}, {x21, x22}}]},
Max@Im@eigs < 10^-12 && Min[Re@eigs] >= 0];
Random section:
SeedRandom[0]; (* for reproducibility *)
normal = Normalize@RandomReal[{-1, 1}, 4, WorkingPrecision -> 20];
point = RandomReal[{0, 10}, 4];
coordsys = Transpose@
N@DeleteCases[Orthogonalize[Join[{normal}, IdentityMatrix[4]]], v_ /; v == {0, 0, 0, 0}];
normal = N@normal;
Check that the point is in the region:
regiondescriptor @@ point
(* True *)
Visualization of the section: The MeshFunctions correspond to the coordinates {x11, x12, x21, x22} to give some idea of the relationship of the section to the X coordinate system.
RegionPlot3D[regiondescriptor @@ (coordsys.{0, z2, z3, z4} + point),
{z2, -20, 80}, {z3, -40, 60}, {z4, -20, 80},
MeshFunctions ->
Function @@@ ({{z2, z3, z4}, #} & /@ (coordsys.{0, z2, z3, z4} + point)),
MeshStyle -> {Black, Cyan, Magenta, Yellow},
AxesLabel -> Automatic]

Another random section through the same point (same RegionPlot code but with the domain {z2, -20, 80}, {z3, -60, 40}, {z4, -80, 20}):
normal = Normalize@RandomReal[{-1, 1}, 4, WorkingPrecision -> 20];
coordsys = Transpose@
N@DeleteCases[Orthogonalize[Join[{normal}, IdentityMatrix[4]]], v_ /; v == {0, 0, 0, 0}];
normal = N@normal;
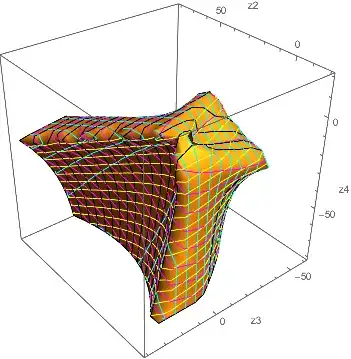
A section orthogonal to the first coordinate axis (RotateLeft[] the matrix to get other axes), plotted over the domain {z2, -50, 50}, {z3, -60, 40}, {z4, -10, 90}.
coordsys = IdentityMatrix[4];
normal = coordsys[[All, 1]];

Update: Plotting the singular section
In response to a comment, here is an approach to plotting the points where the rank of the matrix {{x11, x12}, {x21, x22}} is less than 2.
The idea is to use MeshFunctions to pick out the singular hypersurface Det[{{x11, x12}, {x21, x22}}] == 0. The problem in this case is that it appears to be a boundary of the 4D region. Since RegionPlot3D is discrete (very discrete), I had to fudge a little and pick out the subregion where -0.05 < Det[] < 0.05. (The determinant values are in the low thousands in most of the region, so this represents a relative error of 10^-4 or less.) The following is using the second example, "Another random section." (Of course to get reproducibility, you have to execute the first code again before executing the second.)
RegionPlot3D[regiondescriptor @@ (coordsys.{0, z2, z3, z4} + point),
{z2, -20, 80}, {z3, -60, 40}, {z4, -80, 20},
MeshFunctions -> {Function[{z2, z3, z4},
Det[{{x11, x12}, {x21, x22}}] /.
Thread[{x11, x12, x21, x22} -> (coordsys.{0, z2, z3, z4} + point)] // Evaluate]},
Mesh -> {{-0.05, 0.05}}, MeshShading -> {Magenta, Cyan},
PlotPoints -> 100, AxesLabel -> Automatic]

I suspect that where the cyan is pinched (on the left, in three places) should show nodes (crossing lines). If so, that is an artifact of the fudging and the discretization.