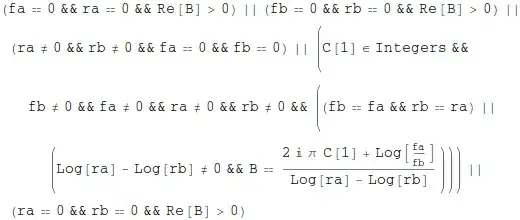Solution of a System of Equations Using `Solve`

Question

Part 1

I am trying to solve a simple system of equations as follows

Solve[{A x^B == f, A y^B == g}, {A, B}]

But I just get the error

Solve::nsmet: This system cannot be solved with the methods available to Solve. >>

I also tried

Reduce[{A x^B == f, A y^B == g}, {A, B}]

to no avail as it lead to an endless evaluation!

I know that in such cases

1- It is a matter of assumptions or conditions that may have not been given to the solver in order to find the solution!

2- Or simply, Solve doesn't know how to solve the equation symbolically due to complexity.

However, I couldn't find any useful assumptions to pass to Mathematica or any complexity. Also, I got excited when I saw that Maple just solved it without any assumptions needed as the following picture shows.

So, what is going on here? :)

Any help is appreciated.

Part 2

I made some progress that is indicated in my answer below. So, please read it before looking to the questions of this part.

The following questions still remained unanswered to me!

1- Why the command

 Reduce[{A x^B == f, A y^B == g}, {A, B}]

does not work here?

2- Why I just cannot get the solution in Real domain by the following command?

 Solve[{A x^B == f, A y^B == g}, {A, B},Reals,MaxExtraConditions -> Automatic]

Trying to plug in some values indicates the Maple solution isn't correct. — Feyre, Jul 03 '16 at 16:29
@Feyre: It seems right to me as I obtained the same result of Maple by hand unless there may be fundamental error! :) — Hosein Rahnama, Jul 03 '16 at 16:33
The numbers I tried did not fulfil reduce constraints as provided by @halirutan — Feyre, Jul 03 '16 at 16:41

score 7 · Accepted Answer · edited Apr 13 '17 at 12:56

7

I think that that the key feature is to use the MaxExtraConditions option for the Solve command.

In elaborate answer of Artes in here, a very very nice presentation is referred. It is entitled as Getting the Most from Algebraic Solvers in Mathematica by Adam Strzeboński. You can download the .cdf file of the presentation which is really helpful. Slide $10$ to $12$ are the ones that exactly discuss this issue.

I think beginners like me will find the answer of the following questions in that representation

1- What is the difference between Reduce and Solve command?
2- What are generic and complete solutions?
3- What are parameters and variables?
4- Why Solve and Reduce command do not accept assumptions on the parameters?

Finally, with the help of the presentation, I found that the command

Solve[{A x^B == f, A y^B == g}, {A, B},MaxExtraConditions -> Automatic]

will give the result.

Also you can just take the Real domain solution by

 Normal[Solve[{A x^B == f, A y^B == g}, {A, B}, MaxExtraConditions -> Automatic]] /. {C[1] -> 0}

edited Apr 13 '17 at 12:56

Community

1

answered Jul 03 '16 at 21:50

Hosein Rahnama

1,727
1
15
29

1

Wow, very good find! I find this option quite counterintuitive. When setting it to Infinity or a number, we get no answer. But setting it to All or Automatic does give an answer. – Szabolcs Jul 04 '16 at 08:18
@Szabolcs: Thanks. :) But Still I didn't get satisfied as I don't know the answer of questions in Part 2. Can you kindly think about them and let me know if you got anything. :) – Hosein Rahnama Jul 04 '16 at 08:20
1

I don't know. Maybe Wolfram will find it useful if you send these examples to them, showing Solve with MaxExtraConditions -> 0, 1, Infinity, All, Automatic and Reduce. Maybe there's a good explanation, maybe something is going wrong ... either way it couldn't hurt to show them the examples. Perhaps there will be a way to improve things in the future. – Szabolcs Jul 04 '16 at 08:25
@Szabolcs: And how can I send them this example? Is there a well known e-mail which receives such examples? :) – Hosein Rahnama Jul 04 '16 at 08:30
2

support(AT)wolfram(DOT)com is what you should try. – J. M.'s missing motivation Jul 04 '16 at 08:34

score 3 · Answer 2 · answered Jul 03 '16 at 16:37

3

Try the following:

eq = Eliminate[{A*ra^B == fa, A*rb^B == fb}, A]
Solve[eq, B]

(* {{B->-(Log[fb/fa]/(Log[ra]-Log[rb]))}} *)

and as you repeat this or do it by hand, please note that there are certain restrictions on the values. If you want to know what Maple did not tell you, try this

Reduce[eq, B]

and look at the conditions that need to be fulfilled

Mathematica graphics

answered Jul 03 '16 at 16:37

halirutan

112,764
7
263
474

2

@H.R. There is much to say, see e.g. What is the difference between Reduce and Solve? – Artes Jul 03 '16 at 17:14
@Artes: Thanks for the valuable link. I read your elaborate answer there. But in this case neither Solve nor Reduce seems to work! :) – Hosein Rahnama Jul 03 '16 at 18:03
@H.R. These both functions work too however one has to input properly right restrictions for variables. Solve can also eliminate variables, e.g. Am I missing anything? Solving Equations – Artes Jul 03 '16 at 18:14
@Artes: What can I do get some answer from Mathematica? Can you kindly write an answer including the right restriction for variables such that it leads to the answer by Maple. :) – Hosein Rahnama Jul 03 '16 at 19:30
@halirutan: A weird thing is that why Reduce[expr,vars] does not work on my original equation without eliminating $A$? Also, Solve[expr,vars,elims] does not work too! – Hosein Rahnama Jul 03 '16 at 20:04

Solution of a System of Equations Using `Solve`

2 Answers2