1

I just got a copy of Mathematica and I'm busy learning the basics. I got mathematica so I can plot hydrogen orbitals but I'm completely lost. I looked around and I found this:

a0 = 1;

ψ[{n_, l_, m_}, {r_, θ_, ϕ_}] :=
  With[{ρ = 2 r/(n a0)}, 
    Sqrt[(2/(n a0))^3 (n - l - 1)!/(2 n (n + l)!)] Exp[-ρ/2] ρ^l 
      LaguerreL[n - l - 1, 2 l + 1, ρ] SphericalHarmonicY[l, m, θ, ϕ]]

DensityPlot3D[
  (Abs @ 
    ψ[
      {3, 2, 0}, 
      {Sqrt[x^2 + y^2 + z^2], ArcTan[z, Sqrt[x^2 + y^2]], ArcTan[x, y]}])^2, 
  {x, -10 a0, 10 a0}, {y, -10 a0, 10 a0}, {z, -15 a0, 15 a0}, 
  PlotLegends -> Automatic]

Can I get a quick explanation of what's going on here? I understand that the first part is just defining the hydrogen wave function, but what about the second part? What does the {Sqrt[x^2 + y^2 + z^2], ArcTan[z, Sqrt[x^2 + y^2]], ArcTan[x, y]} term do? Also, is the Abs @ the absolute square of the wave function?

Community
  • 1
Ayumu Kasugano
  • 111
  • 3
  • 1
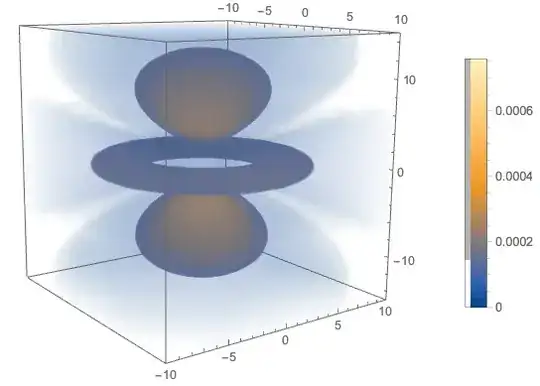
    Please state where you got the code from. If it was on this site, make sure to include a link (not just to give credit to the author, but also to be able to get better explanations). The questions you're asking should be obvious if you look at the documentation for Abs and DensityPlot3D (the latter uses Cartesian coordinates, whereas the wave function is in spherical coords.) – Jens Jul 07 '16 at 18:33
  • 1
    Oops, right here: http://mathematica.stackexchange.com/a/88150/41521 – Ayumu Kasugano Jul 07 '16 at 18:34
  • 1
    I'm sure @xslittlegrass will be able to explain the code if necessary. Bu I think what I mentioned above are the main points. – Jens Jul 07 '16 at 18:37
  • Yes, but not very obvious to me. I get that they are converting spherical to cartesian. I get how r=sqrt[x^2+y^2+z^2] but what does ArcTan[z,sqrt[x^2+y^2]] mean? Is this a conversion to $\theta$? Why is there a comma placed inside? – Ayumu Kasugano Jul 07 '16 at 18:47
  • Check the documentation for ArcTan with two arguments; it gives the arc tan of the ratio taking into account which quadrant it is in. – QuantumDot Jul 07 '16 at 19:24
  • 1
    Whenever you use code that is not originally yours, please remember to link to where you got it from. – J. M.'s missing motivation Jul 07 '16 at 23:55

1 Answers1

2
  1. Abs @expresion is the prefix notation for Abs[expresion]

  2. The 2nd argument of ψ indicates that it wants spherical coordinates. 

    {Sqrt[x^2 + y^2 + z^2], ArcTan[z, Sqrt[x^2 + y^2]], ArcTan[x, y]}

    is just transforming a point given in Cartesian coordinates into spherical coordinates.

  3. I don't see the need for Abs @. 

DensityPlot3D[
  ψ[{3, 2, 0},
    {Sqrt[x^2 + y^2 + z^2], ArcTan[z, Sqrt[x^2 + y^2]], ArcTan[x, y]}]^2,
  {x, -10 a0, 10 a0}, {y, -10 a0, 10 a0}, {z, -15 a0, 15 a0},
  PlotLegends -> Automatic]

gives the same plot as your code.

plot

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
  • Thank you! What is the comma in the ArcTan[z, Sqrt[x^2 + y^2]] and ArcTan[x, y]}]^2 terms supposed to mean? Aren't we just converting $\theta = \arccos{\frac{z}{r}}$ and $\phi=\arctan{\frac{y}{x}}$? Plus, shouldn't we be plotting $4\pi r^2 \psi ^2$ to get the probability density? – Ayumu Kasugano Jul 07 '16 at 18:57
  • @AyumuKasugano. Please look up ArcTan in the Documentation Center. You will find it has a two-argument form in Mathematica that resolves quadrant ambiguities. – m_goldberg Jul 07 '16 at 19:03
  • Ah, but those aren't the correct conversions? $\theta$ isn't $\arctan{\frac{z}{\sqrt{x^2+y^2}}}$ and $\phi$ isn't $\arctan{\frac{x}{y}}$? – Ayumu Kasugano Jul 07 '16 at 19:13
  • @AyumuKasugano. Then I don know what is going on. Remember, I didn't write the code. – m_goldberg Jul 07 '16 at 19:18
  • 2
    @Ayumu, please look up atan2 in Wikipedia. This is the correct way to do angle conversions instead of taking the arctangent of a ratio. – J. M.'s missing motivation Jul 07 '16 at 23:47