Sketch the dual lattice $\Gamma^*$?

Question

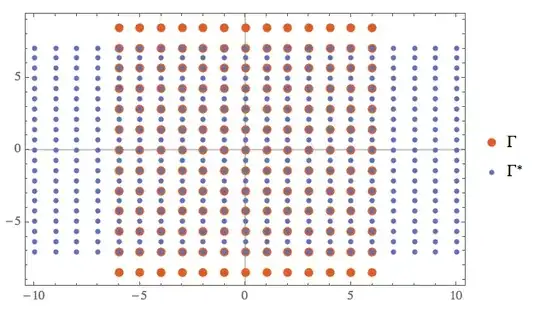
In the book Eigenvalues in Riemannian Geometry of Isaac Chavel page $28$ - $29$, they talk about the lattice $\Gamma$ and it is defined as $$\Gamma = \left\{\sum_{j=1}^n \alpha^j v_j : \alpha^j \in \mathbb{Z}, j=1,\dots, n\right\}.$$ If I take the canonical basis (simplifying the problem) $v_1=(1,0)$, $v_2=(0,\sqrt{2})$, then I obtain $\Gamma=\begin{pmatrix} 1 & 0 \\ 0 & \sqrt{2} \end{pmatrix}\mathbb{Z}^2$. Now, it is possible to associate to the lattice $\Gamma,$ the dual lattice, $\Gamma^*$, given by $$\Gamma^*=\{y \in \mathbb{R}^n : \langle x,y\rangle \in \mathbb{Z} \text{ for all } x \in \Gamma\}.$$

Questions : Does it exist a way to interpret the dual lattice $\Gamma^*$ graphically, a sketch? How should we interpret this concept in the resolution of the spectrum on the torus?

Thanks!

Welcome! I suggest the following:

As you receive help, try to give it too, by answering questions in your area of expertise.

Take the tour and check the faqs!

When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — , Jul 08 '16 at 12:44
Just to make sure, this is a question about how to sketch this specifically with the software Mathematica, right? — Szabolcs, Jul 08 '16 at 15:03
Yes, but I don't have any experience with this software. I'd like a sketch to better understand the concept of dual lattice $\Gamma^*$ in correspondence with his lattice $\Gamma$ — Desharnais David, Jul 08 '16 at 15:04
What have you tried. Please post the code and point out where you're having issues. — Jens, Jul 08 '16 at 16:49
I'll wait if someone know the subject, and yes, $\langle x,y \rangle$ is the usual inner product — Desharnais David, Jul 08 '16 at 17:41
You could do an inversion of an associated matrix, as noted here. After that, you can adapt my solution here. — J. M.'s missing motivation, Jul 08 '16 at 22:49

score 2 · Accepted Answer · answered Jul 09 '16 at 00:28

Here is one way to do the visualization. It is some sort of brute force, direct application of the definitions.

Define lattice $\Gamma$ generation vectors:

v1 = {1, 0};
v2 = {0, Sqrt[2]};

Generate some $\Gamma$ points:

With[{c = 6}, 
  points = Flatten[Outer[#1 v1 + #2 v2 &, Range[-c, c], Range[-c, c]], 1]];

Make a "dual lattice point finder" function:

ls = LinearSolve[{v1, v2}];

Find dual lattice $\Gamma^*$ points by complete enumeration of a subset of $\mathbb{Z}$:

With[{c = 10}, 
  dualPoints = 
   ls /@ Flatten[Outer[List, Range[-c, c], Range[-c, c]], 1]];

Verify according to definition that the points belong to $\Gamma^*$:

Tally[Map[And @@ Map[IntegerQ, points.#] &, dualPoints]]
(* {{True, 441}} *)

Plot the points from both lattices:

ListPlot[{points, dualPoints}, 
 PlotStyle -> {{PointSize[0.02]}, {PointSize[0.012]}},
 PlotTheme -> "Scientific", 
 PlotLegends -> {"\[CapitalGamma]", 
   "\!\(\*SuperscriptBox[\(\[CapitalGamma]\), \(*\)]\)"}]

@J.M. I did not know that function. I was thinking to justify not using it with "I am trying to be more didactic in my answer," but I realized I am not sure what someone with math background, but new to Mathematica would prefer: solutions with a small set of core functions, or solutions with minimal code that is clear from the function names what it does. — Anton Antonov, Jul 09 '16 at 00:41

Sketch the dual lattice $\Gamma^*$?

1 Answers1