Dealing with numerical integration singularities

Question

I'm trying to perform the following integral (numerically)

(1)

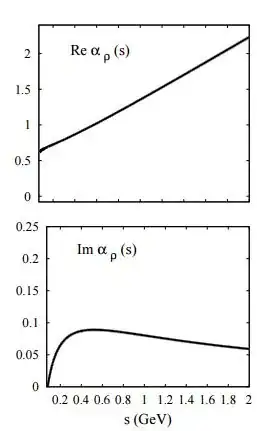
And their behaviour is

where PV denotes principal Value.

In principle I don't know the functions $\rm{Im}(\alpha)$ and $\rm{Re}(\alpha)$, but I know their behaviour between $s=0$ and $s=2$. I just need to know if the equation (1) from above is correct. For that purpose I made my own function of $\rm{Im}(\alpha)$ that behaves like the figure shown (I called it $\alpha$ first)

alpha[s_] = rho[s] (0.12 E^-(0.35 s));

where

rho[s_] = Sqrt[1 - 4 m^2/s];

and

m = 0.13957;

Then I made an interpolation to the function (just to practice numerical integration with known points of a function)

Tab1 = Table[{s, alpha[s]}, {s, 4 m^2, 2, 0.001}];
im = Interpolation[Tab1] ;

Supposing that at this point everything is all right, I have some points of my function and I want to deal with the numerical integration (1) shown above.

I divided the two first terms of the $\rm{Re}(\alpha)$:

step = (2 - 0.14^2)/20;
si = Table[4 m ^2 + (i - 1) step, {i, 1, 21}];
ai = Table[{si[[i]], {0.520 + 0.902 si[[i]]}}, {i, 1, 21}];

and the integration part goes as follows:

bi = 
  NIntegrate[Table[im[s]/(s (s - si[[i]])), {i, 1, 21}], {s, 4 m^2, 2}, 
    Method -> PrincipalValue]

Obiously this integration doesn't give the result I wanted because I have to specify in which points the denominator goes to zero (so it can apply the PV).

Here comes my question. This $bi$ diverges everytime $s=si$. How can I specify in my function these points? I tried using the option

Method -> {"PrincipalValue", "SingularPointsIntegrationRadius" -> }]

but it seems Mathematica 9 (the one I'm using) doesn't have this option. I also tried taking few points and specifying the singular points, but the function also diverges when $s$ tends to $si$ so it doesn't work either. Does someone have any idea how to do it?

P.S.: I don't want to specify what the variables mean because it's a much larger problem.

What do you mean when it "tends to" si? Do you have a specific distance from the values of si s needs to get to for the function to diverge? Otherwise I'd say Exclusions -> Thread[si == s] — Feyre, Jul 09 '16 at 10:22
@Feyre Thank you very much. The specification of the singular points got fixed with Thread as you said. Now it says ' NIntegrate::nlim: "s = s==0.09902 is not a valid limit of integration"' I've been looking at it and can't find why that point is not valid. Sorry about the edition but I'm new here. — Jordi, Jul 10 '16 at 09:28

Feyre · Accepted Answer · 2016-07-10T14:18:50.210

Table[NIntegrate[
  im[s]/(s (s - SetPrecision[si[[i]], MachinePrecision])), {s, 4 m^2, 
   2}, Method -> "PrincipalValue", Exclusions -> si[[i]] == s,
   MaxRecursion -> 500], {i, 1, 21}]

{2.70869, 0.196226, -0.196659, -0.300094, -0.328605, -0.331732, -0.325217, -0.315038, -0.303723, -0.292415, -0.281655, -0.271706, -0.262715, -0.254788, -0.248052, -0.242715, -0.239182, -0.238366, -0.242852, -0.266702, -0.241464}

We can check the validity of the result with a hacky workaround:

si = SetPrecision[si, MachinePrecision];
a = Table[
  NIntegrate[im[s]/(s (s - si[[i]])), {s, si[[i]] + 0.00001, 2}], {i, 
   1, 21}];
b = Prepend[
  Table[NIntegrate[
    im[s]/(s (s - si[[i]])), {s, 4 m^2, si[[i]] - 0.00001}], {i, 2, 
    21}], 0];
a+b

{2.70624, 0.196262, -0.196637, -0.300081, -0.328596, -0.331725, -0.325213, -0.315035, -0.30372, -0.292413, -0.281653, -0.271705, -0.262713, -0.254787, -0.248051, -0.242714, -0.239182, -0.238365, -0.24285, -0.266702, -0.274749}

Which as expected yields a close match.

Dealing with numerical integration singularities

1 Answers1