Join data point with arrows in ErrorListPlot

Question

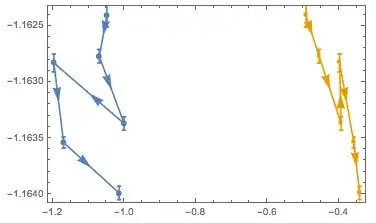
the data is

Needs["ErrorBarPlots`"];

data={{{{-1.04845, -1.16241}, ErrorBar[0.0001]}, {{-1.06996, -1.16277}, 
   ErrorBar[0.00006]}, {{-1.00061, -1.16337}, 
   ErrorBar[0.00006]}, {{-1.19685, -1.16283}, 
   ErrorBar[0.00008]}, {{-1.1696, -1.16354}, 
   ErrorBar[0.00005]}, {{-1.01451, -1.16399}, 
   ErrorBar[0.00006]}}, {{{-0.49151, -1.16241}, 
   ErrorBar[0.0001]}, {{-0.45521, -1.16277}, 
   ErrorBar[0.00006]}, {{-0.39356, -1.16337}, 
   ErrorBar[0.00006]}, {{-0.39785, -1.16283}, 
   ErrorBar[0.00008]}, {{-0.35805, -1.16354}, 
   ErrorBar[0.00005]}, {{-0.34185, -1.16399}, ErrorBar[0.00006]}}}

And I plot it with

ErrorListPlot[data,
  Frame -> True, PlotMarkers -> {Automatic}, Joined -> True, 
 Mesh -> All, PlotRange -> All]

which gives

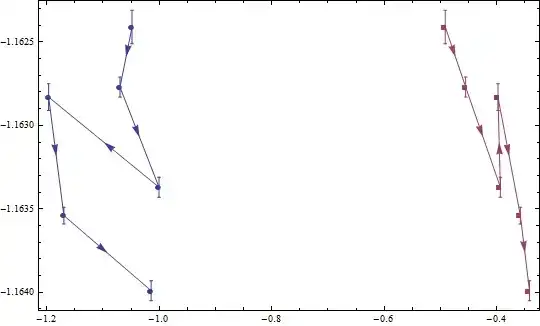
I want to add arrow in the middle of each line of this plot to show the evolution of data like below

What is the best way to do this?

http://mathematica.stackexchange.com/questions/60838/adding-arrows-in-curves and http://mathematica.stackexchange.com/questions/97813/how-to-add-arrows-in-the-middle-of-the-plot-lines — Young, Jul 13 '16 at 04:30
@march Hi, march. Sorry for my mistake. Thank you for correcting it. — matheorem, Jul 13 '16 at 06:14

score 4 · Accepted Answer · edited Jul 13 '16 at 06:39

4

I usually modify plots using the following methods. It's rarely automated, but it works. The plan is to replace the Lines in the Graphics object represented by the figure with Arrows, but we need to find them first.

First, we use the data in the OP and name the function plt:

plt = ErrorListPlot[data,
       Frame -> True, PlotMarkers -> {Automatic},
       Joined -> True, Mesh -> All, PlotRange -> All];

Then, we want to extract from the plot all Graphics primitives that are Lines using

Cases[Normal[plt], _Line, Infinity]

The first three elements of this list are

{Line[{{-1.04845, -1.16241}, {-1.06996, -1.16277}, {-1.00061, -1.16337}, {-1.19685, -1.16283}, {-1.1696, -1.16354}, {-1.01451, -1.16399}}],
 Line[{{-1.04845, -1.16231}, {-1.04845, -1.16251}}], 
 Line[{Offset[{1.5, 0}, {-1.04845, -1.16231}],
 ... }

The first element is the Line joining the points (and there is another one later on). The second element is the vertical error bar, and the third is one of either the top or lower horizontal bars in the error bar. We only want to extract the Lines joining the points, so we do

Cases[Normal[plt], Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2, Infinity]
(* {Line[{{-1.04845, -1.16241}, {-1.06996, -1.16277}, {-1.00061, -1.16337}, {-1.19685, -1.16283}, {-1.1696, -1.16354}, {-1.01451, -1.16399}}],
    Line[{{-0.49151, -1.16241}, {-0.45521, -1.16277}, {-0.39356, -1.16337}, {-0.39785, -1.16283}, {-0.35805, -1.16354}, {-0.34185, -1.16399}}]} *)

That's them! So we modify the plot as follows:

plt
  /. Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2
      :> {Arrowheads[{{0.05, 0.5}}], Arrow /@ Partition[a, 2, 1]}

resulting in

edited Jul 13 '16 at 06:39

matheorem

17,132
8
45
115

answered Jul 13 '16 at 04:31

march

23,399
2
44
100

Hi, march. Thank you very much for your answer. I learned a lot of clever tricks from your answer. One thing I don't understand is Normal. I never thought Normal could apply to a plot ! It seems that this is not documented and I still haven't figured out what exactly has Normal done to a plot. for example, I found Cases[plt, Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2, Infinity] only got {Line[{1, 2, 3, 4, 5, 6}], Line[{7, 8, 9, 10, 11, 12}]} – matheorem Jul 13 '16 at 06:39
@matheorem, Normal[] converts GraphicsComplex[] objects (which are usually produced by plotting functions) into an explicit list of primitives and directives. You can search the site for many examples of its use. – J. M.'s missing motivation Jul 13 '16 at 06:41
@J.M. Hi, J.M. That is still not clear. Why Normal[plt] deletes the errorbar? – matheorem Jul 13 '16 at 06:43
You can answer that yourself, @matheorem. Ponder on the result of FreeQ[ErrorListPlot[(* stuff *)], _ErrorBar]. – J. M.'s missing motivation Jul 13 '16 at 06:46
@J.M. Nope. The plt is free from ErrorBar head already, the errorbar is drawn by Line. What I mean is that why Normal[plt] output a plot without a errorbar line? You said "Normal[] converts GraphicsComplex[] objects", but you didn't mean it will change the plot, right? – matheorem Jul 13 '16 at 06:55
That seems to be a bug in either Normal[] or GraphicsComplex[]; the Line[]s with Offset[] coordinates get removed for some reason. Here is a simpler example: GraphicsComplex[{{-1, 0}, {1, 0}}, {Line[{1, 2}], Line[{Offset[{0, -10}, {0, 0}], Offset[{0, 10}, {0, 0}]}]}] // Normal. – J. M.'s missing motivation Jul 13 '16 at 06:57
@J.M. I now got a little confused with answer of march. Have you notice Cases[Normal@plt, Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2, Infinity] and Cases[plt, Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2, Infinity] produce different result. As I said before, the latter gives {Line[{1, 2, 3, 4, 5, 6}], Line[{7, 8, 9, 10, 11, 12}]} which is not the right line data we want. But plt/. Line[a_?(FreeQ[#, Offset] &)] /; Length[a] > 2 :> {Arrowheads[{{0.05, 0.5}}], Arrow /@ Partition[a, 2, 1]} weirdly produces the right plot with arrow? Why? Am I missing something? – matheorem Jul 13 '16 at 07:05
@matheorem. As for your last question, it seems like ReplaceAll automatically "Normalizes" the plot so that it can match the patterns correctly. This seems like a good choice for the implementation of ReplaceAll, since GraphicsComplexes are hard to parse. – march Jul 13 '16 at 16:25
@march Hi, march. Interesting behavior of ReplaceAll. But as J.M has pointed out there seems to be a bug in either Normal[] or GraphicsComplex[] cause the removal of Offset[]. As I understand it, your code seems relying on the bug removal of Offset[], am I right? – matheorem Jul 15 '16 at 02:02
@matheorem. I'm not really sure, actually. With these kinds of things, I usually just inspect things, try various patterns, and extract things until they work. It's very much trial and error. – march Jul 15 '16 at 02:29
@march I see. Yeah, trial and error, daily experiences : ) – matheorem Jul 15 '16 at 02:35

score 4 · Answer 2 · answered Jul 13 '16 at 08:44

4

llp = ListLinePlot[data[[All, All, 1]], Frame -> True, 
    PlotStyle -> Arrowheads[{0, .025, 0}], PlotRange -> All] /.
   Line[x_] :> (Arrow@Partition[x, 2, 1]);

elp = ErrorListPlot[data, PlotMarkers -> {Automatic}, Joined -> False];

Show[llp, elp]

Mathematica graphics

answered Jul 13 '16 at 08:44

kglr

394,356
18
477
896

Oh, using Show! Clever trick. Upvoted : ) – matheorem Jul 15 '16 at 02:04
I never thought Arrowheads could be put into PlotStyle, it is undocumented, right? – matheorem Jul 15 '16 at 02:07
@matheorem, thank you for the vote. Since Arrowheads is a graphics directive, it can be used in PlotStyle. There is an example in the documentation: Arrow >> Properties & Relations – kglr Jul 15 '16 at 02:16
Thank you, kglr. It is just too many things can put into "Style", I never succeeded in figuring them out clearly. : ) – matheorem Jul 15 '16 at 02:31

Join data point with arrows in ErrorListPlot

2 Answers2