How to fill outside instead of inside graphical shapes?

Question

I want to omit parts of Graphics from scenes by defining a geometric shape where details are visible, a "keyhole" of sorts, and fill all the rest as one would do to insides of the regular graphics primitives. How to accomplish this?

My best effort example this far is below, and there are several issues with it.

ClearAll[showWithHole];

showWithHole[g_Graphics, face_, edge_, shape_Graphics] := 
 With[{invreg = 
    RegionDifference[FullRegion[2], DiscretizeGraphics[shape]],
   opts = AbsoluteOptions[g]},
  Show[g, Graphics[
    {FaceForm[face], EdgeForm[], 
     MeshPrimitives[
      DiscretizeRegion[invreg, 1.1 PlotRange /. opts, 
       MeshQualityGoal -> "Minimal"], 2],
     edge, 
     MeshPrimitives[
      BoundaryDiscretizeRegion[invreg, 1.1 PlotRange /. opts], 1]}], 
   Sequence @@ opts]]

EDIT:

Some improvements (particularly, hairlines are now gone!):

ClearAll[showWithHole];

showWithHole[g_Graphics, face_, edge_, shape_Graphics] := 
 With[{invreg = 
    RegionDifference[FullRegion[2], DiscretizeGraphics[shape]],
   opts = AbsoluteOptions[g]},
  Show[g, Graphics[
    {FaceForm[face], EdgeForm[edge], 
     FilledCurve[
      BoundaryDiscretizeRegion[invreg, 
         CoordinateBounds[Transpose[PlotRange /. opts], 
          Scaled[0.05]]]["BoundaryPolygons"] /. 
       Polygon[pts_] :> {Line[pts]}]}], Sequence @@ opts]]

showWithHole[
 Graphics[{Blue, Disk[{1, 0}, 3/2]}],
 Directive[Opacity[1/2], White], Red,
 Graphics[{Disk[{0, 0}, 1], 
   FilledCurve[{{Line@CirclePoints[{2, 1}, 1/2, 6]},
                {Line@CirclePoints[{2, 1}, 1/4, 6]}}]}]]

EDIT 2:

[This is now split into an answer below.]

Answers with less kludgy approach (especially avoiding geometric region discretization step!) are still welcome.

@YvesKlett Unedited version suffers from sides of polygons on partially transparent area being visible (but edited version fixes that). Issues with discretization of "complex" shapes is another problem, and in this case shows up on the circle being clearly edgy, and sometimes even discretized polygons lose some sides. — kirma, Jul 17 '16 at 11:23
I think this would be better presented as a question and answer, as with edit 2 you appear to have a fully working solution. — Simon Woods, Jul 17 '16 at 13:55
@SimonWoods I don't particularly like that solution, but yes, I should split it to a candidate answer. — kirma, Jul 17 '16 at 13:58
@Wjx Please write an answer based on it! It seems that HighlightImage and FilledCurve based methods provide somewhat different subsets of styling, though. Also, a big drawback for HighlightImage is that it requires Images, when working with vector Graphics would be more quality-friendly. — kirma, Jul 18 '16 at 04:16
@kirma yes, Image stuff lose quality. I will write an answer later as now I'm at sxhool — Wjx, Jul 18 '16 at 04:32
@kirma I've posted an answer but It seems that HighlightImage simply refuse to work with FilledCurve I strongly suspect that is a bug. Also, the quality of the image is quite good. — Wjx, Jul 18 '16 at 13:33
@Wjx Interesting, this complete omission of FilledCurve in the implementation! I'd assume it to work. Interestingly JoinedCurve does sort of work. I might assume this is caused by wrong item somewhere in internal pattern matching for graphics primitives. Have you reported a bug on this? — kirma, Jul 18 '16 at 14:19
nope, I'm wondering whether should I post a new question confirming whether this do is a bug. — Wjx, Jul 18 '16 at 14:20
@Wjx Go ahead, somebody used to spelunking with Mma internals might provide insight on this! :) — kirma, Jul 18 '16 at 14:21
These two approaches both have their own unique advantages and drawbacks, Interesting!!! — Wjx, Jul 18 '16 at 14:21

kirma · Accepted Answer · 2016-07-17T14:18:51.603

This answer is split from evolution of the question. In its core, it relies on BoundaryDiscretizeGraphics to create polygons defining holes (note, these may be inside each other), and properties of FilledCurve with polygons inside each other to perform the intended "filling of the outside." Parts of data given to FilledCurve intentionally extend outside PlotRange, in order not to frame the plot with EdgeForm.

ClearAll[showWithHole];

showWithHole[g_Graphics, face_, edge_, shape_Graphics, 
  discoptions : OptionsPattern[BoundaryDiscretizeGraphics]] :=
 Module[{opts, scaledbounds},
  opts = AbsoluteOptions[g];
  scaledbounds = 
   CoordinateBounds[Transpose[PlotRange /. opts], Scaled[0.1]];
  Show[g, Graphics[
    {FaceForm[face], EdgeForm[edge], 
     FilledCurve[
      Prepend[BoundaryDiscretizeGraphics[shape, 
          PlotRange -> scaledbounds, discoptions][
         "BoundaryPolygons"] /. 
        Polygon[pts_] :> {Line[pts]}, {Line[
         Tuples[scaledbounds][[{1, 2, 4, 3}]]]}]]}], 
   Sequence @@ opts]]

showWithHole[
 Graphics[{Red, Disk[{1, 0}, 3/2]}],
 Directive[Opacity[9/10], White], Black, 
 Graphics[{Disk[{0, 0}, 1], 
   FilledCurve[{{Line@CirclePoints[{2, 1}, 1/2, 6]},
                {Line@CirclePoints[{2, 1}, 1/4, 6]}}]}],
 MaxCellMeasure -> 0.001]

Wjx · Answer 2 · 2016-07-18T14:11:25.263

I finally got home and finished my answer, but there's still one drawback which I strongly suspect as a bug of HighlightImage. So, I'll present you a partial solution now:

Clear["`*"];
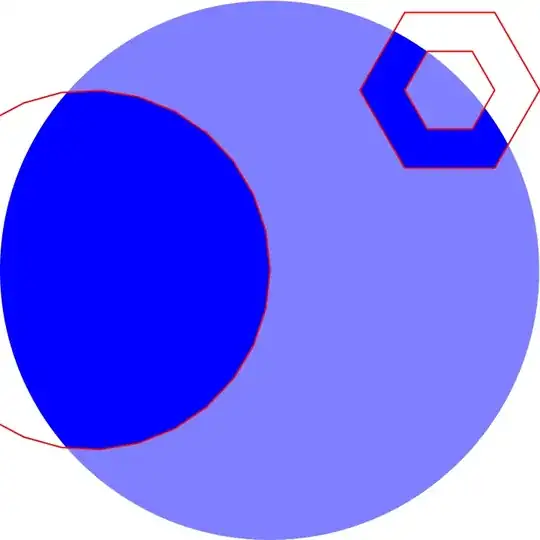
img = Graphics[{Blue, Disk[{1, 0}, 3/2]}];
mask = {Disk[{0, 0}, 1], Polygon[CirclePoints[{2, 1}, 1/2, 6]]};

range = AbsoluteOptions[img, PlotRange][[1, 2]];
trans[{x_, y_}] := 
 Scaled@{(x - range[[1, 1]])/(range[[1, 2]] - range[[1, 1]]), (y - 
      range[[2, 1]])/(range[[2, 2]] - range[[2, 1]])}
tsize[{x_, y_}] := 
 Scaled@{x/(range[[1, 2]] - range[[1, 1]]), 
   y/(range[[2, 2]] - range[[2, 1]])}

(*Attention: while using Arrow, only the first form is allowed. Do \
not support ***Triangle series*)
rep = {(f : (Point | Line | HalfLine | InfiniteLine | BezierCurve | 
         BSplineCurve | Arrow | Triangle | Polygon | RegularPolygon | 
         Rectangle | Parallelogram | Simplex))[x_] :> 
    f[x /. e : {ax_?NumericQ, ay_?NumericQ} :> 
       trans@e], (f : (Disk | Circle))[cen_: {0, 0}, r_: {1, 1}, 
     angle_: {0, 2 Pi}] :> 
    f[trans[cen], If[Head[r] === List, tsize[r], tsize[{r, r}]], 
     angle]};

HighlightImage[Rasterize@img, mask /. rep, {"Lighten", .5}]

This result differs from what you need a bit, I will make clear of that later.

Usage

img is the original Graphics or Plot (It also okay when using Image content, but you may need to specify the range by yourself). Feel free to put anything here.
mask is mask. There's some restrictions here: You cannot use ***Triangle as It's hard to define it after some scaling or so, also, maybe There'll be some strange function I didn't add in. Most Graphics primitives are all okay, so feel free to add something here as well.
style can be adjusted in HighlightImage, check the documentation and find out everthing about customizing this part.

How it works

The key part is to scale the mask, so I used most of the code to convert everything into Scaled form:

Extract the PlotRange option using:

range = AbsoluteOptions[img, PlotRange][[1, 2]];

Create simple scaling functions:

trans function aims to transform point coordinates and tsize function aims to transform the relative positions.

trans[{x_, y_}] := 
 Scaled@{(x - range[[1, 1]])/(range[[1, 2]] - range[[1, 1]]), (y - 
      range[[2, 1]])/(range[[2, 2]] - range[[2, 1]])}

tsize[{x_, y_}] := 
 Scaled@{x/(range[[1, 2]] - range[[1, 1]]), 
   y/(range[[2, 2]] - range[[2, 1]])}

Implement the scaling transform to multiple functions:

Lots of funtions like Point or Line always use absolute coordinates, so simple transformation will be ediquate. but Disk and Circle shall need a bit more special attention.

rep = {(f : (Point | Line | HalfLine | InfiniteLine | BezierCurve | 
         BSplineCurve | Arrow | Triangle | Polygon | RegularPolygon | 
         Rectangle | Parallelogram | Simplex))[x_] :> 
    f[x /. e : {ax_?NumericQ, ay_?NumericQ} :> 
       trans@e], (f : (Disk | Circle))[cen_: {0, 0}, r_: {1, 1}, 
     angle_: {0, 2 Pi}] :> 
    f[trans[cen], If[Head[r] === List, tsize[r], tsize[{r, r}]], 
     angle]};

Create the combined image:

 HighlightImage[Rasterize@img, mask /. rep, {"Lighten", .5}]

Some other issue

This approach offers a different set of customization. For example, you can blur, desaturate, Lighten, Darken, remove inner and outer region.

Clear["`*"];
img = Graphics[
   Table[{Hue[t/15, 1, .9, .3], 
     Disk[4 {Cos[2 Pi t/15], Sin[2 Pi t/15]}, 4]}, {t, 15}]];
mask = Graphics[
   Table[{Disk[(8 - r) {Cos[2 Pi q/12], Sin[2 Pi q/12]}, 
      Sqrt[(8 - r)]*(Sqrt[q] + 1)/15]}, {r, 6}, {q, 12}]];

range = AbsoluteOptions[img, PlotRange][[1, 2]];
trans[{x_, y_}] := 
 Scaled@{(x - range[[1, 1]])/(range[[1, 2]] - range[[1, 1]]), (y - 
      range[[2, 1]])/(range[[2, 2]] - range[[2, 1]])}
tsize[{x_, y_}] := 
 Scaled@{x/(range[[1, 2]] - range[[1, 1]]), 
   y/(range[[2, 2]] - range[[2, 1]])}

(*Attention: while using Arrow, only the first form is allowed. Do \
not support ***Triangle series*)
rep = {(f : (Point | Line | HalfLine | InfiniteLine | BezierCurve | 
         BSplineCurve | Arrow | Triangle | Polygon | RegularPolygon | 
         Rectangle | Parallelogram | Simplex))[x_] :> 
    f[x /. e : {ax_?NumericQ, ay_?NumericQ} :> 
       trans@e], (f : (Disk | Circle))[cen_: {0, 0}, r_: {1, 1}, 
     angle_: {0, 2 Pi}] :> 
    f[trans[cen], If[Head[r] === List, tsize[r], tsize[{r, r}]], 
     angle]};

HighlightImage[img, mask /. rep, {"Desaturate", .7}] // AbsoluteTiming

A result with desaturate effect, this effect is hard to achieve by Graphics I suppose?

It's said in the documentation that the second part of HighlightImage can be any form of Graphics primitives, but whenever a FilledCurve Primitive is presented, HighlightImage will refuse to create filling. Also, Blur option will even ignore Polygons or so. Quite confusing, isn't it?

Is it a bug?

emmm, the poor quality of the figure is due to the poor screenshot, not the real quality of the image. In fact, the final image is of quite high resolution and accuracy. — Wjx, Jul 18 '16 at 13:32

How to fill outside instead of inside graphical shapes?

2 Answers2

Usage

How it works

Some other issue

Linked