Intersection coordinates of two spheres

Question

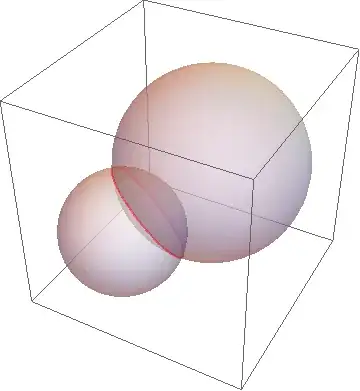
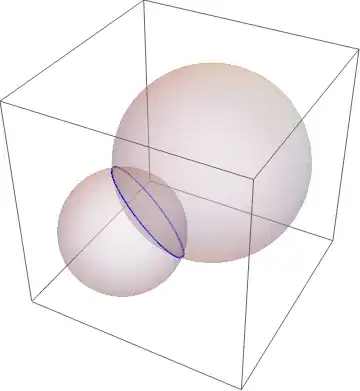
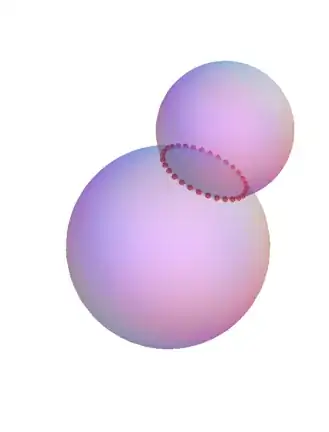
I am trying to obtain a list of coordinates at which two spheres intersect.

Take for example the spheres: sp1=Sphere[{0, 0, 0}, 1] and sp2=Sphere[{1, 1, 1}, 1.5] When I Plot them it is clear they intersect, but i cannot retrieve the coordinates.

So far I Tried finding them by looking for the nearest or RegionNearest between RandomPoint[Sphere[{0, 0, 0}, 1], 1000] and RandomPoint[Sphere[{1, 1, 1}, 1.5],1000]. Nor did it work by looking for Intersection of the two list (since no coordinates actually matched) I also tried to look for the minimal euclidean distance between all points and the positions of those minimal distances, but in that case my computer crashes. Can somebody help? Thanks in advance

This seems simple enough to compute analytically (pen and paper) that it might not be worth bothering with the numerical approach ... — Szabolcs, Jul 20 '16 at 12:05
it takes just a little tweaking to generalize that mathworld solution to the case where the spheres are not along a coordinate axis.. — george2079, Jul 20 '16 at 12:20
In my example it is simple enough for pen and paper, but i want to do it for 180 different and more complicated spheres, which makes it useful to be able to let mathematica take care of it. And I had seen the sphere sphere intersection explanation and notebook, but dont see how i can apply it to my spheres. — B.Seppen, Jul 20 '16 at 12:24
What do you mean by "a list of coordinates" for the intersection? Just sampling the region? — kirma, Jul 20 '16 at 14:47

score 6 · Answer 1 · edited Jul 28 '17 at 11:52

6

sp1 = Sphere[{0, 0, 0}, 1];
sp2 = Sphere[{1, 1, 1}, 1.5];
ri1 = RegionIntersection[sp1, sp2];
l = MeshCoordinates[DiscretizeRegion[ri1]];
Show[Graphics3D[{Opacity[0.5], sp1, sp2, Thick, Red, 
   Line@l[[Last[FindShortestTour[l]]]]}]]

Note that you can find the center and radius of the circle with:

o = Mean[l];
r = Mean[Table[Norm[l[[i]] - Mean[l]], {i, Length[l]}]];

The normal of the circle is naturally in the direction of either of the centers of the spheres.

edited Jul 28 '17 at 11:52

J. M.'s missing motivation

124,525
11
401
574

answered Jul 20 '16 at 13:30

B.Seppen

119
6

+1 - Now the question is, can you reorder the points so that they can be used in a Line, via Graphics3D[{Opacity[0.5], sp1, sp2, Red, Thick, Line@l}]? – Jason B. Jul 20 '16 at 14:06
@JasonB added the center and radius of the circle. Unfortunately Circle[] doesn't work in 3D. – Feyre Jul 20 '16 at 14:48
1

@Feyre - it seems in this example you can use FindShortestTour: This works: Graphics3D[{Opacity[0.5], sp1, sp2, Red, Thick, Line@l[[Last@FindShortestTour@l]]}] – Jason B. Jul 20 '16 at 14:50
@JasonB Yes, updated the answer – Feyre Jul 20 '16 at 15:02

score 4 · Answer 2 · edited Apr 13 '17 at 12:55

This answer uses the circle3D function written by Taiki, found here. But it specifically does not use any of the Region functionality to find the intersection. Instead, I just grabbed some formulas from this MathWorld page

circle3D[centre_: {0, 0, 0}, radius_: 1, normal_: {0, 0, 1}, angle_: {0, 2 Pi}] :=
  Composition[
    Line,
    Map[RotationTransform[{{0, 0, 1}, normal}, centre], #] &,
    Map[Append[#, Last@centre] &, #] &,
    Append[DeleteDuplicates[Most@#], Last@#] &,
    Level[#, {-2}] &,
    MeshPrimitives[#, 1] &,
    DiscretizeRegion,
    If
  ][
    First@Differences@angle >= 2 Pi,
    Circle[Most@centre, radius],
    Circle[Most@centre, radius, angle]
  ]

sphereIntersection[{x1_, r1_}, {x2_, r2_}] := 
  Module[{dvec, d, d1, r},
   dvec = x2 - x1;
   d = Norm@dvec;
   d1 = (d^2 + r1^2 - r2^2)/(2 d);
   circle3D[x1 + d1 Normalize[x2 - x1], Sqrt[r1^2 - d1^2], 
    Normalize[x2 - x1]]
   ];
sphereIntersection[s1_Sphere, s2_Sphere] := 
 sphereIntersection[List @@ s1, List @@ s2]

Using the OP's spheres, you can visualize it via

Graphics3D[{Opacity[.3], sp1, sp2, Opacity[1], Blue, Thick, 
  sphereIntersection[sp2, sp1]}]

Mathematica graphics

You can grab the points via

Cases[Graphics3D[sphereIntersection[sp2, sp1]], 
 Line[{a__}] :> a, Infinity]

or just get random points via

RandomPoint[sphereIntersection[sp2, sp1]]

J. M.'s missing motivation · Answer 3 · 2016-07-21T01:05:15.847

Using the results from this MathWorld page:

BlockRandom[SeedRandom["spherical"];
            c1 = RandomReal[1, 3]; c2 = RandomReal[1, 3];
            r2 = RandomReal[3/2]; r1 = RandomReal[3/2];
            d = EuclideanDistance[c1, c2];
            u = (d^2 + r1^2 - r2^2)/(2 d^2); cc = {1 - u, u}.{c1, c2}; 
            rc = Sqrt[r1^2 - d^2 u^2];
            Graphics3D[{Opacity[1/2], Sphere[c1, r1], Sphere[c2, r2],
                        {Red, Tube[BSplineCurve[
                                   AffineTransform[{RotationMatrix[{{0, 0, 1},
                                                    Normalize[c2 - c1]}], cc}][
                                   rc PadRight[{{1, 0}, {1, 1}, {0, 1}, {-1, 1},
                                                {-1, 0}, {-1, -1}, {0, -1}, {1, -1},
                                                {1, 0}}, {Automatic, 3}]], 
                                   SplineClosed -> True, SplineDegree -> 2, 
                                   SplineKnots -> {0, 0, 0, 1/4, 1/4, 1/2,
                                                   1/2, 3/4, 3/4, 1, 1, 1},
                                   SplineWeights -> {1, 1/Sqrt[2], 1, 1/Sqrt[2], 1,
                                                     1/Sqrt[2], 1, 1/Sqrt[2], 1}]]}},
                       Boxed -> False]]

two intersecting spheres

Here's a variation using CirclePoints[] to evenly sample the circle:

BlockRandom[SeedRandom["spherical"];
            c1 = RandomReal[1, 3]; c2 = RandomReal[1, 3];
            r2 = RandomReal[3/2]; r1 = RandomReal[3/2];
            d = EuclideanDistance[c1, c2];
            u = (d^2 + r1^2 - r2^2)/(2 d^2); cc = {1 - u, u}.{c1, c2};
            rc = Sqrt[r1^2 - d^2 u^2];
            n = 30;
            Graphics3D[{Opacity[1/2], Sphere[c1, r1], Sphere[c2, r2],
                        {Red, Sphere[AffineTransform[{RotationMatrix[{{0, 0, 1},
                                                      Normalize[c2 - c1]}], cc}][
                                     PadRight[ArrayPad[CirclePoints[rc, n],
                                                       {{0, 1}, {0, 0}}, "Periodic"],
                                              {Automatic, 3}]], 1/100]}}, Boxed -> False]]

crown of spheres

@Jason, it was just a means to an end. ;) Let me edit this to include a variation... — J. M.'s missing motivation, Jul 21 '16 at 00:52

score 2 · Answer 4 · answered Jul 20 '16 at 14:50

2

If you want to simply sample the intersection, you can do this:

RandomPoint[
   ImplicitRegion[
    RegionMember[
     RegionIntersection[Sphere[{0, 0, 0}, 1], 
      Sphere[{1, 1, 1}, 1.5]], {x, y, z}], {x, y, z}], 100] // 
  Point // Graphics3D

This should work, but maybe it doesn't because of the single-dimensional nature of the sampling region:

RandomPoint[
     RegionIntersection[Sphere[{0, 0, 0}, 1], 
      Sphere[{1, 1, 1}, 3/2]], 100] // Point // Graphics3D

answered Jul 20 '16 at 14:50

kirma

19,056
1
51
93

Also, you can construct actual solutions for equations involved around RegionMember, but that needs more specific information of what you're really after. – kirma Jul 20 '16 at 15:15

score 1 · Answer 5 · edited Jul 22 '16 at 04:39

Why not just generate the parametric equations for the intersection of the spheres? You know that the intersection points form a circle in a plane perpendicular to the vector between the centers of the spheres.

sphereIntersection[{x1_, r1_}, {x2_, r2_}, th_] :=

  Module[{dvec, d, d1, r, rr, ss, nx, ny, nz},
   dvec = x2 - x1;
   d = Norm@dvec;
   dvec = {nx, ny, nz} = Normalize@dvec;
   d1 = (d^2 + r1^2 - r2^2)/(2 d);
   If[r1^2 < d1^2, Return[$Failed]];
   r = Sqrt[r1^2 - d1^2];
   rr = {1 - nx^2/(1 + nz), -nx ny/(1 + nz), -nx};
   ss = {-nx ny/(1 + nz), 1 - ny^2/(1 + nz), -ny};
   x1 + d1 dvec + r (Cos[th] rr + Sin[th] ss)];
sphereIntersection[s1_Sphere, s2_Sphere, th_] := 
 sphereIntersection[List @@ s1, List @@ s2, th]

You get your equation via

sphereIntersection[sp1, sp2, theta] // FullSimplify
(* {(
 7 (3 + Sqrt[3]) + Sqrt[143] (3 + 2 Sqrt[3]) Cos[theta] - 
  Sqrt[429] Sin[theta])/(24 (3 + Sqrt[3])), (
 7 (3 + Sqrt[3]) - Sqrt[429] Cos[theta] + 
  Sqrt[143] (3 + 2 Sqrt[3]) Sin[theta])/(24 (3 + Sqrt[3])), 
 1/24 (7 - Sqrt[143] Cos[theta] - Sqrt[143] Sin[theta])} *)

And generate points via

sphereIntersection[sp1, sp2, #] & /@ Range[0, 2 π, π/2] // N
(* {{0.972304, 0.109291, -0.206594}, {0.109291, 
  0.972304, -0.206594}, {-0.38897, 0.474043, 
  0.789928}, {0.474043, -0.38897, 0.789928}, {0.972304, 
  0.109291, -0.206594}} *)

And plot it via

Show[Graphics3D[{Opacity[0.2], sp1, sp2}],
 ParametricPlot3D[
  sphereIntersection[sp1, sp2, theta], {theta, 0, 2 π}, 
  Evaluated -> True]
 ]

Mathematica graphics

@J.M. Thanks, it's better without using a random number to generate the basis vectors — Jason B., Jul 21 '16 at 20:49
I know; I was actually trying to look for this paper when I saw your solution. Apart from that little typo I've now fixed, it's pretty nice! — J. M.'s missing motivation, Jul 22 '16 at 01:30

Intersection coordinates of two spheres

5 Answers5

Linked