Generate a certain colorful triangle

Question

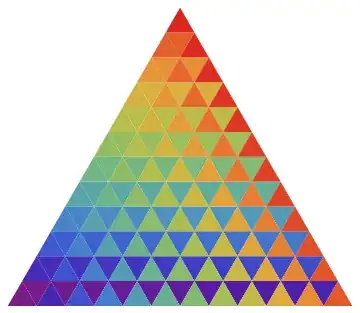
I want to get a colorful triangle like this:

I hope to get a triangle with any number of layers. This is my current method. Actually, I'm not very content with these graph theory functions, since I have to use Quiet to mute the error information.

pointPair = Subsets[{{0, 0}, {1, Sqrt[3]}, {2, 0}}, {2}];
midPoint[{a_, b_}, {c_, d_}, n_] := 
 Transpose[{Subdivide[a, c, n], Subdivide[b, d, n]}]
layers = 8;(*Control the layers*)
poly = Polygon /@ 
  FindClique[
   Quiet[NearestNeighborGraph[
     Level[RegionIntersection @@@ 
       Subsets[Line /@ 
         Transpose /@ 
          MapAt[Reverse, 
           Subsets[midPoint[##, layers] & @@@ pointPair, {2}], {2, 
            2}], {2}], {3}]]], {3}, All];
Graphics[Transpose[{RandomColor[Length[poly]], poly}]]

Answer 1

I am late to see this question but here is a solution closely based on my answer to Creating a Sierpinski gasket with the missing triangles filled in.

tri[n_] :=
  Table[{2 j - i, Sqrt[3] i}, {i, 0, n}, {j, i, n}] // 
    Partition[Riffle @@ #, 3, 1] & /@ Partition[#, 2, 1] &

Example of use:

Map[{RandomColor[], Polygon@#} &, tri[5], {2}] // Graphics

---

A different approach

For some reason I found this problem unusually interesting so that even after "solving" it I was thinking about it. It occurred to me that the total number of triangles is $n^2$ therefore I wanted to make a function that could generate these from a call to Array rather than Table. (The latter permits non-rectangular indices as used in my first method.)

My method is to reflect the triangles that fall outside of target back inside.

fn[n_] := Array[fn, {n, n}]

fn[i_, j_] /; j > i := fn[j, i + 1, -1]

fn[x_, y_, s_: 1] :=
  { 2 x - y + {0, 1, 2}, Sqrt[3] {y, s + y, y} }\[Transpose] // Polygon

Map[{RandomColor[], #} &, fn[7], {2}] // Graphics

• Note: by design every triangle is generated separately which is not as efficient as my first approach which generates entire rows in one operation.

Keeping the coloration separate allows some interesting flexibility. Coloring sequentially provides a pleasing effect due to the order of generation.

Module[{i = 0},
  Map[{ColorData["Rainbow"][i++/144], #} &, fn[12], {2}] // Graphics
]

Color based on the array coordinates:

Array[{Hue[##/400, #/7, #2/7], fn @ ##} &, {7, 7}] // Graphics

Answer 2

I guess something like this:

With[{n = 7},
     BlockRandom[SeedRandom["triangles"];
                 Graphics[Table[{RandomColor[],
                                 RegularPolygon[{Sqrt[3] (j + i - 1),
                                                 3 j + Boole[EvenQ[i]]}/2,
                                                {1, (-1)^i π/6}, 3]},
                                {i, 2 n - 1}, {j, n - Quotient[i, 2]}]]]]

Answer 3

This question is not a bit hard:

mat = {{1, 0}, {1/2, Sqrt[3]/2}};
draw[n_] := 
  Graphics[Table[{RandomColor[], 
       Triangle[{{i + n + 1 - #, j + n + 1 - #}, {i, j + 1}, {i + 1, 
           j}}.mat]}, {i, n}, {j, # - i}] & /@ {n, n + 1}];
draw[8]

Code is easy, check it by yourself~

Answer 4

Anothor way by NestList

randomTriPlot[n_] := Module[{next},
  next[polys_] := 
   Join[Map[# + {-1, -Sqrt[3]} &, 
     polys, {2}], {MapAt[# - 2 Sqrt[3] &, 
      polys[[-1]], {1, 2}], # + {1, -Sqrt[3]} & /@ polys[[-1]]}];
  (*get coordinate of the next layer by translate this layer*)
  Flatten@
    Map[Polygon, 
     NestList[next, N@{{{0, 0}, {-1, -Sqrt[3]}, {1, -Sqrt[3]}}}, 
      n - 1], {2}] // Graphics[Thread[{RandomColor[Length@#], #}]] &
  ]
randomTriPlot[7]

Answer 5

Using the trick in this answer to use MeshFunctions and Dynamic MeshShading with random colors:

coloredTriangles = ParametricPlot[{x, y Sqrt[3] Min[x, 2 - x]}, {x, 0, 2}, {y, 0, 1}, 
     MeshFunctions -> {Sqrt[3] # + #2 &, #2 - Sqrt[3] # &, #2 &}, 
     Mesh -> # - 1, Exclusions -> None, ImageSize -> 200,
     MeshShading -> Dynamic@{{{RandomColor[], RandomColor[]}, {RandomColor[], 
              RandomColor[]}}}, Frame -> False, Axes -> False] &;

Examples:

Row[coloredTriangles /@ {3, 4, 6, 8}, Spacer[5]]

Answer 6

Clear["Global`*"];
SeedRandom[1];

(* r1 splits a triangle into four parts using Midpoint functionality*)

r1 = Triangle[{a_, b_, c_}] :> Sequence[
    Triangle[{a, Midpoint[{a, c}], Midpoint[{a, b}]}]
    , Triangle[{b, Midpoint[{b, c}], Midpoint[{b, a}]}]
    , Triangle[{c, Midpoint[{c, a}], Midpoint[{c, b}]}]
    , Triangle[{Midpoint[{a, c}], Midpoint[{a, b}], Midpoint[{b, c}]}]
    ];

itri = Triangle[{{0, 0}, {2, 0}, {1, Sqrt[3]}}];    
tris = First@#[[Length@# ;;]] &@NestList[# /. r1 &, {itri}, 3];
Graphics[{Riffle[RandomColor[Length@tris], tris]}]

---

3D view

itri = Triangle[{{0, 0}, {2, 0}, {1, Sqrt[3]}}];
SeedRandom[2];
r2 = Triangle[{{a1_, a2_}, {b1_, b2_}, {c1_, c2_}}] :> Triangle[{
     {a1, a2, Log[1/4, Area[Triangle[{{a1, a2}, {b1, b2}, {c1, c2}}]]]}
     , {b1, b2, 
      Log[1/4, Area[Triangle[{{a1, a2}, {b1, b2}, {c1, c2}}]]]}
     , {c1, c2, 
      Log[1/4, Area[Triangle[{{a1, a2}, {b1, b2}, {c1, c2}}]]]}
     }];
tris3 = NestList[# /. r1 &, {itri}, 3] /. r2 // Flatten;
tris3D = Riffle[RandomColor[Length@tris3], tris3];
Graphics3D[{Opacity[0.5], tris3D}
 , Axes -> True
 , AxesLabel -> {"x", "y", "z"}
 ]