This is not a question which I estimate is aided in answering by providing complete code, which is excessively long.
I ran an NDSolve[] at MachinePrecision, with the specification MaxSteps -> ∞. I then plotted the step size used:
ListPlot[stepsd, PlotRange -> All]
I thought the step size was disconcertingly high, especially since I was trying to eliminate numerical errors in the output yet the NDSolve[] ran very fast:
AbsoluteTiming[s = NDSolve[Flatten[{xf, yf, zf,vel, pos}], Flatten[{xt, yt, zt}], {t, 0, time}, MaxSteps -> ∞];]
{0.748079, Null}
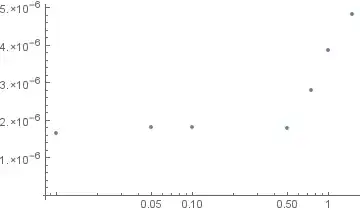
Consequently I decided to make a graph of the end numerical error (I know the real values to 17 digit precision at the end point) in relation to MaxStepSize ->α:
Note that this is error of the form $$\sigma=\sqrt{\sigma^2_x+\sigma^2_y+\sigma^2_z}$$
ListLogLinearPlot[Transpose[{α, σ}]]
As you can see the error plummets to about one third, and stays there when the MaxStepSize is reduced to 0.5 or lower, at which point I suspect the model error starts to dominate (the model is of course not perfect). The timing for 0.5 is:
{1.20144, Null}
As the starting values used for this part are between $O[1]$ and $O[-4]$, and are given with 17 digit precision (though Mathematica registers the dataset at MachinePrecision, I'm surprised this numerical error is allowed as the documentation centre claims that:
NDSolve adapts its step size so that the estimated error in the solution is just within the tolerances specified by PrecisionGoal and AccuracyGoal.
Am I missing something, or did the NDSolve[] fail to accurately pick an appropriate MaxStepSize?

NDSolveuses [NDSolve`ScaledVectorNorm[2, {10.^-pg, 10.^-ag}]](http://reference.wolfram.com/language/tutorial/NDSolveVectorNorm.html), (pg,ag=PrecisionGoal,AccuracyGoalsettings resp.) to measure the acceptability of the estimated error. (2) The estimated error is an estimate, and not guaranteed to bound the actual error. -- Some clarification about howσis computed would be helpful. – Michael E2 Jul 24 '16 at 15:10AUanddayunits. – Feyre Jul 24 '16 at 15:39Precisionwhich is halfWorkingPrecision. Am I to understand that with the available information it cannot be guaranteed that the model delivers 7-digit precision as I expected? – Feyre Jul 24 '16 at 15:4810.^-pg * * solutionor10.^-ag: In the first case, relative error will dominate, and in the second, absolute error will dominate. When they're about the same, then the (absolute) error tolerance will be about two times10^-ag. (This is just a consequence of the formula in the tutorial I linked above.) So the answer to your question depends on whether you're talking about absolute or relative error (if the solution has a numerical magnitude of about1., then they're roughly the same). – Michael E2 Jul 24 '16 at 16:391and value0, the z component stays in the-4order for the duration of this calculation. However it is the x and y components that have the higher order errors. – Feyre Jul 24 '16 at 16:47NDSolve[]), and that sometimes is a problem. For this sort of problem, a symplectic integrator is often used; see this tutorial. – Michael E2 Jul 24 '16 at 16:47NDSolvecontrols. If you have many steps, those errors can add up if they're mainly in one direction. – Michael E2 Jul 24 '16 at 17:10