How to efficiently implement k-FN (k-Furthest Neighbors)?

Question

I'd like to pick k points from a set of points in n-dimensions that are approximately "maximally apart" (sum of pairwise distances is almost maxed). What is an efficient way to do this in MMA? Using the solution from C Woods, for example:

KFN[list_, k_Integer?Positive] := Module[{kTuples},
    kTuples=Subsets[RandomSample[list,Max[k*2,100]],{k}, 1000];
    MaximalBy[kTuples,Total[Flatten[Outer[EuclideanDistance[#1,#2]&,#,#,1]]]&]
]
pts=RandomReal[1,{100,3}]
kfn=KFN[pts,3][[1]]
Graphics3D[{Blue,Point[pts],PointSize[Large],Red,Point[kfn]}]

But here's the catch: I need this algorithm to be efficient enough to scale to this size:

pts=RandomReal[1,{10^6,10^3}];
kfn=KFN[pts,100]
Graphics3D[{Blue,Point[pts],PointSize[Large],Red,Point[kfn]}]

Notes

1. The comment from J.M. works for k=2, but hangs at k=4.

2. Here's a nice paper on k-FN:

   • http://www.dcs.gla.ac.uk/workshops/ddr2012/papers/p3said.pdf

Answer 1

Here is a naive solution that can be slow for large lists of points:

KFN[list_, k_Integer?Positive] := Module[{kTuples},
  kTuples = Subsets[list, {k}];
  MaximalBy[kTuples, 
   Total[Flatten[Outer[EuclideanDistance[#1, #2] &, #, #, 1]]] &]
  ]

(Use of Subsets function thanks to N.J. Evans. ) I'm not convinced there is a computationally "efficient" solution for this problem, but there are probably better algorithms than the one I have given you.

Answer 2

Not necessarily best of quality but maybe could be made better with a bit of tuning.

kDistant[pts_List, n_] := Module[
  {objfun, len = Length[pts], ords, a, c1},
  ords = Array[a, n];
  c1 = Flatten[{Map[.5 <= # <= len + .5 &, ords], 
     Element[ords, Integers]}];
  objfun[oo : {_Integer ..}] := Module[
    {ovals = Clip[oo, {1, len}], ptlist, diffs},
    ptlist = pts[[ovals]];
    diffs = 
     Flatten[Table[
       ptlist[[j]] - ptlist[[k]], {j, n - 1}, {k, j + 1, n}], 1];
    Total[Map[Sqrt[#.#] &, diffs]]
    ];
  Round[NArgMax[{objfun[ords], c1}, ords, 
    Method -> {"DifferentialEvolution", "SearchPoints" -> 40}, 
    MaxIterations -> 400]]
  ]

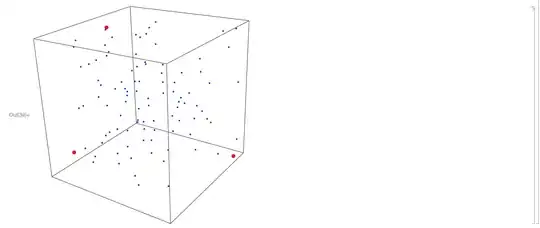
Example searching for 10 from 100000 points.

n = 10;
len = 10^5;
pts = RandomReal[{-10, 10}, {len, 3}];

Timing[furthest = kDistant[pts, n]]

(* Out[6]= {15.85276, {34502, 90523, 79761, 66318, 53570, 18000, 80585, 
  12958, 87680, 70241}} *)

Seems to have done alright, points tend toward corners. Some pairs are close but that's probably an indication that the objective is not the best to use for k large.

Graphics3D[{Red, PointSize[Large], Point[pts[[furthest]]]}]

--- edit ---

The variant below might be better for some purposes. Instead of maximizing a sum of all disatnce pairs it will maximize the sum of all minimum separations, which should have the effect of pushing all points away from one another. Some experimentation led me to increase iterations and also slightly up the number of points.

kDistantMins[pts_List, n_] := Module[
   {objfun, len = Length[pts], ords, a, c1},
   ords = Array[a, n];
   c1 = Flatten[{Map[.5 <= # <= len + .5 &, ords], 
      Element[ords, Integers]}];
   objfun[oo : {_Integer ..}] := Module[
     {ovals = Clip[oo, {1, len}], ptlist, diffs, dnorms, minnorms},
     ptlist = pts[[ovals]];
     diffs = 
      Table[ptlist[[j]] - ptlist[[k]], {j, n - 1}, {k, j + 1, n}];
     dnorms = Map[Sqrt[#.#] &, diffs, {2}];
     minnorms = Map[Min, dnorms];
     Total[minnorms]];
   Round[NArgMax[{objfun[ords], c1}, ords, 
     Method -> {"DifferentialEvolution", "SearchPoints" -> 50}, 
     MaxIterations -> 1000]]
   ];

Whether this turns out to be an improvement will depend on the end goal I guess.

--- end edit ---

Answer 3

It is possible to write the total distance between the k points as a quadratic form based on the DistanceMatrix M. Finding the k points that maximise the total distance between them is then a matter of finding a vector V of zeros and ones that maximises V.M.V and whose total is k .

The following uses a literal implementation of this idea

kfn[list_, k_Integer?Positive] :=
 Module[{M, V, v, n, sol},
  n = Length[list];
  M = DistanceMatrix[list];
  V = Array[v, n];
  sol = NMaximize[{V.M.V, Total[V] == k, Thread[0 <= V <= 1], 
     Element[V, Integers]}, V];
  Pick[list, Thread[V == 1] /. Last[sol]]
  ]

This is not very useful. It appears to be slower and less reliable than KFN by @C.Woods (repeated to make the answer self-contained)

KFN[list_, k_Integer?Positive] := Module[{kTuples},
  kTuples = Subsets[list, {k}];
  MaximalBy[kTuples, 
   Total[Flatten[Outer[EuclideanDistance[#1, #2] &, #, #, 1]]] &]
  ]

However, we can relax the requirement that the vector V contains only integers (but still have 0 <= V <= 1), to give a function

candidate[list_, k_Integer?Positive] :=
 Module[{M, V, v, n, sol},
  n = Length[list];
  M = DistanceMatrix[list];
  V = Array[v, n];
  sol = FindMaximum[{V.M.V, Total[V] == k, Thread[0 <= V <= 1]}, V, 
    Gradient -> 2 M.V, Method -> "QuadraticProgramming"];
  Pick[list, Thread[V > 0.001] /. Last[sol]]
  ]

that picks out a list of points whose length is typically a little more than k. Note that this is a concave/convex problem with a unique global solution. When fed with this list of points KFN is much faster (and in limited testing, gives the same answer). For example:

 pts = RandomReal[1, {100, 3}];
 AbsoluteTiming[KFN[pts, 3];]
 (* {1.78323, Null} *)
 AbsoluteTiming[KFN[candidate[pts, 3], 3];]
 (* {0.239304, Null} *)
 AbsoluteTiming[KFN[pts, 4];]
 (* {63.4595, Null} *)
 AbsoluteTiming[KFN[candidate[pts, 4], 4];]
 (* {0.306873, Null} *)

I have no proof that candidate is guaranteed to pick a subset containing the solution, but it seems plausible that it should give good (if not optimal) candidates.

This certainly won't scale to the higher number of points requested in the OP, but since the size of the optimisation problem is independent of the dimensionality of the space in which the points lie, it should cope with high dimensional spaces.