Translate graphics from a contour plot to tile a plane

Question

MWE:

a = {3, Sqrt[3]}/2;
b = {3, -Sqrt[3]}/2;
W = Parallelogram[{0, 0}, {a, b}];

img = ContourPlot[Sqrt[x^2 + 5 Cos[x^2 y]]^2, {x, y} ∈ W, AspectRatio -> Automatic]

This produces the contour plot of some given function over the region W, which is defined as the primitive unit cell of the Bravais lattice spanned by lattice vectors a and b, seen here:

Show[
ContourPlot[Sqrt[x^2 + 5 Cos[x^2 y]]^2, {x, y} ∈ W, 
AspectRatio -> Automatic, PlotRange -> {{-2, 5}, {-2, 2}}],
Graphics[{Green, Arrow[{(a + b)/2, (a + b)/2 + a}]}],
Graphics[{Magenta, Arrow[{(a + b)/2, (a + b)/2 + b}]}]
]

I wish to produce a plot in which I show several copies of this contour plot, tiled at locations given by small-integer multiples of the lattice vectors.
In other words, how can I translate my contourplot by vector a and show it in the same plot region as the original, with the axes shown?

I have tried many things related to GeometricTransformation but without success. Such as

trans = GeometricTransformation[img, TranslationTransform[a]]  

Show[img, trans]

etc.

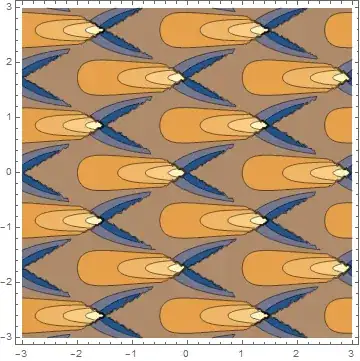
Try this: trans =. img /. GraphicsComplex[xs__] :> GeometricTransformation[GraphicsComplex[xs], TranslationTransform[a]]; Show[img, trans, PlotRange -> {{0, 6}, {-2, 2}}] — march, Aug 05 '16 at 17:52
That's because there was a typo. Change trans =. img ... to trans = img ... (there was an extra .). — march, Aug 05 '16 at 18:03

score 3 · Answer 1 · answered Aug 05 '16 at 18:18

Figuring out the mechanism behind the following is left as an exercise for the interested reader:

With[{a = {3, Sqrt[3]}/2, b = {3, -Sqrt[3]}/2}, 
     ContourPlot[Function[{x, y}, Sqrt[x^2 + 5 Cos[x^2 y]]^2] @@
                 (Mod[LinearSolve[Transpose[{b, a}], {x, y}], 1].{b, a}),
                 {x, -3, 3}, {y, -3, 3}]]

tiles

score 3 · Accepted Answer · answered Aug 05 '16 at 19:40

3

Since GeometricTransformation only works on GraphicsPrimitives, we take advantage of the fact that the default expression-form of figures involve GraphicsComplexes and that those are primitives:

Show[Table[img /.
     With[{n = n, m = m}, 
       GraphicsComplex[xs__]
        :> GeometricTransformation[GraphicsComplex[xs], TranslationTransform[n a + m b]]
      ],
      {n, -2, 2}, {m, -2, 2}],
   PlotRange -> All]

answered Aug 05 '16 at 19:40

march

23,399
2
44
100

Thanks, this works well for me and is mostly transparent. Can you elaborate on the xs__ argument? Specifically, you use two "_". I assume you are somehow pointing it to go inside img, which is a plot, and find all the GraphicComplexes, but how did you know to do this in this way? – Steve Aug 08 '16 at 14:44

Translate graphics from a contour plot to tile a plane

2 Answers2