Technique for drawing polyhedron cutaway

Question

Here is a graphic I drew with an earlier version of Mathematic (probably version 6) which I no longer have available:

At the time Polyhedra was an external package, and I produced the cut-away by truncating a list of component polyhedra of the truncated icosahedron before drawing.

Recent versions of Mathematica have an entirely different (and now integrated) set of polyhedron functions, that look nothing like what I used before. Can anyone suggest a strategy for redrawing this figure now?

Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! — Michael E2, Aug 09 '16 at 00:39
I guess you're referring to PolyhedronData["TruncatedIcosahedron"]? — Michael E2, Aug 09 '16 at 00:42
Do you still have the old code, at least? Can you elaborate on how you "truncat(ed) a list of component polyhedra of the truncated icosahedron"? — J. M.'s missing motivation, Aug 09 '16 at 04:42

score 5 · Answer 1 · edited Apr 13 '17 at 12:55

An adaptation of my answer here:

SeedRandom[3]; (* for reproducibility *)
With[{poly = PolyhedronData["TruncatedIcosahedron"] /. 
    Polygon[pp_] :> Polygon[RandomSample[pp, 24]]}, 
 With[{r0 = PolyhedronData["TruncatedIcosahedron", "Circumradius"],
       r1 = 1,                   (* input: r1 = inner boundary vertex distance *)
       r2 = 2},                  (* input: r2 = outer boundary vertex distance *)
  With[{pts = First@Cases[poly, 
       GraphicsComplex[p_, e__] :> Flatten[{p *(r1/r0), p*(r2/r0)}, 1],
       Infinity]}, 
   Graphics3D[GraphicsComplex[pts,
     {EdgeForm[], Lighter@ColorData[97, 2],
      Cases[poly, Polygon[p_] :> Polygon@Join[p, p + Length[pts]/2], Infinity], 
      Cases[poly, 
       Polygon[p_] :> Polygon[
          Flatten[
           Join[#, Reverse@# + Length[pts]/2] & /@ Partition[#, 2, 1, 1] & /@ p,
           1]],
       Infinity]}
     ], PlotRange -> All, Options[poly]]]]]

Mathematica graphics

cvgmt · Answer 2 · 2024-03-06T03:55:41.660

We remove the neiborhoods of one of the face of TruncatedIcosahedron.
After we select the polygons, we add the original {0,0,0} to each polygons and use ConvexHullMesh to construct some pyramid.

adjfaces = 
 PolyhedronData["TruncatedIcosahedron", "AdjacentFaceIndices"]
face = 1;
indexs = 
  Complement[adjfaces // Flatten // DeleteDuplicates, 
   Select[adjfaces, MemberQ[#, face] &] // Flatten // 
    DeleteDuplicates];
polys = PolyhedronData["TruncatedIcosahedron", "Polygons"][[indexs]];
Graphics3D[{polys /. 
   Polygon[pts_] :> ConvexHullMesh[Append[pts, {0, 0, 0}]], 
  SphericalPlot3D[1, {θ, 0, Pi}, {ϕ, 0, 2  Pi}][[1]]}, 
 Boxed -> False]

To view the sphere, we remove one more polygon.

Clear["Global`*"];
adjfaces= PolyhedronData["TruncatedIcosahedron", "AdjacentFaceIndices"];
g = UndirectedEdge @@@adjfaces//Graph;
face = 1;
indexs1 = AdjacencyList[g, face, 1];
indexs2 = AdjacencyList[g, face, 2];
indexs = 
  Complement[VertexList[g], 
   Join[{face}, indexs1, {Complement[indexs2, indexs1][[5]]}]];
polys = PolyhedronData["TruncatedIcosahedron", "Polygons"][[indexs]];
Graphics3D[{polys /. 
   Polygon[pts_] :> ConvexHullMesh[Append[pts, {0, 0, 0}]], 
  SphericalPlot3D[1, {θ, 0, Pi}, {ϕ, 0, 2 Pi}][[1]]}, 
 Boxed -> False]

kglr · Answer 3 · 2023-03-26T03:18:13.863

Remove faces visible from a given view point and extrude the remaining faces:

ClearAll[visibleVerts, facesKept, intrudeFace]
visibleVerts[viewp_] := Intersection[
   MeshCoordinates[#], 
   MeshCoordinates[
    RegionDifference[ConvexHullMesh[Prepend[MeshCoordinates[#], viewp]], #]]] &
facesKept[viewp_] := Select[x |-> DisjointQ[x[[1]], visibleVerts[viewp] @ #]] @ 
  MeshPrimitives[#, 2] &
intrudeFace[scaledThickness_, p_ : {0, 0, 0}] := ConvexHullMesh[Join[First @ #, 
    ScalingTransform[(1 - scaledThickness) {1, 1, 1}, p] @ First @ #], ##2] &

Examples:

{bmr, cb} = PolyhedronData["TruncatedIcosahedron",
   {"BoundaryMeshRegion", "CoordinateBounds"}];
zh = 1.2;
vp = {0, 0, zh cb[[-1, -1]] };
t = .3;
Row[{Graphics3D[{Opacity[.5], Red, facesKept[vp][bmr]}, 
    Boxed -> False, ImageSize -> Medium], 
  Show[intrudeFace[t] /@ facesKept[vp][bmr], ImageSize -> Medium],
  Show[intrudeFace[t][#, MeshCellStyle -> {{2, All} :> RandomColor[]}] & /@ 
    facesKept[vp][bmr], 
  Graphics3D[{Red, 
   Ball[{0, 0, 0},
     (1 - t) PolyhedronData["TruncatedIcosahedron", "Circumradius"]]}],
  ImageSize -> Medium]}, 
 Spacer[10]]

Use zh = 1.5 to get

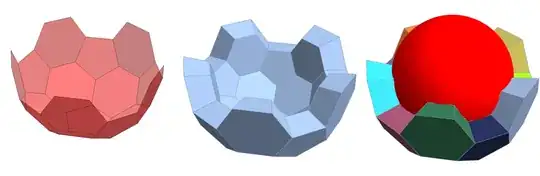
and zh = 4 to get

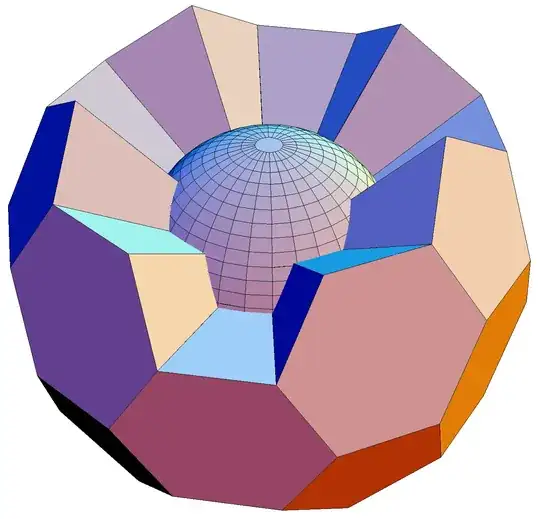
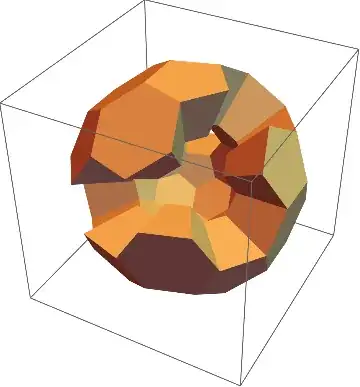
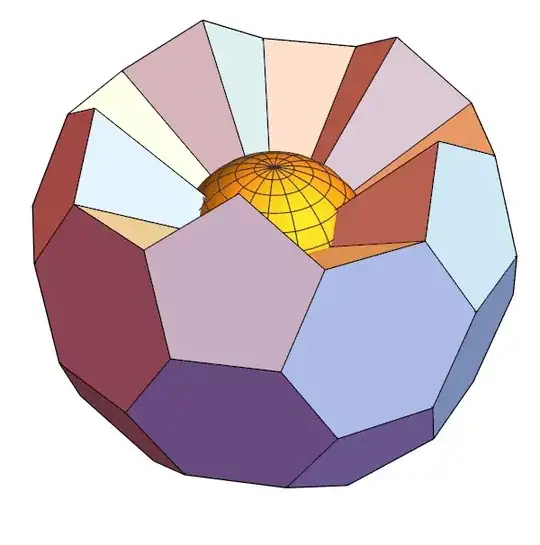
With zh = 1.1 combined with varies thickness values we get

Multicolumn[
 Table[Show[intrudeFace[s] /@ facesKept[vp][bmr], 
   Lighting -> "Neutral", ImageSize -> Medium, 
   PlotLabel -> Row[{"thicknes: ", s}]], {s, {.1, .3, .5, 1}}], 
 2, Dividers -> All, Appearance -> "Horizontal"]

Technique for drawing polyhedron cutaway

3 Answers3