Best fit curve for a data file

Question

I have the following dataset

Data = {{0, 7.77238*10^-43}, {10, 4.80845*10^-14}, {20, 1.83671*10^-13}, {30, 3.79201*10^-13}, {40, 5.87258*10^-13}, {50,7.47558*10^-13}, {60, 8.14542*10^-13}, {70, 7.90253*10^-13}, {80, 7.1244*10^-13}, {90, 6.1629*10^-13}}

The curve look like this

The plot is generated by joining the points. I want best fit, a continious plot.

Your data seems to be miscopied, the brackets don't work properly. Also I would recommend checking out the documentation, notably: http://reference.wolfram.com/language/tutorial/CurveFitting.html — ktm, Aug 10 '16 at 13:15
Duplicate of http://mathematica.stackexchange.com/questions/30492/find-a-best-fitting-curve-for-some-data-with-no-regular-pattern — QuantumBrick, Aug 10 '16 at 13:17
Note that it is often wise to reform your data in better units: data = Times[#, {1, 10^13}] & /@ data;, this can lead to better results when doing fitting. — Feyre, Aug 10 '16 at 13:27

score 7 · Accepted Answer · edited Aug 10 '16 at 13:47

Simple NonlinearModelFit

data = {{0, 7.77238*10^-43}, {10, 4.80845*10^-14}, {20, 
    1.83671*10^-13}, {30, 3.79201*10^-13}, {40, 5.87258*10^-13}, {50, 
    7.47558*10^-13}, {60, 8.14542*10^-13}, {70, 7.90253*10^-13}, {80, 
    7.1244*10^-13}, {90, 6.1629*10^-13}};

model = a x + b x^2 + c x ^3 + d x^4 + e;

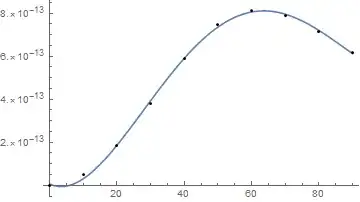
nlm = NonlinearModelFit[data, model, {a, b, c, d, e}, x]

Plot[nlm[x], {x, 0, 90}, Epilog -> Point[data], PlotRange -> All]

6.8861328671318974*^-15-7.317406274281032*^-15 x+1.1455851486013915*^-15 x^2-1.8092531662781587*^-17 x^3+7.885912004661972*^-20 x^4

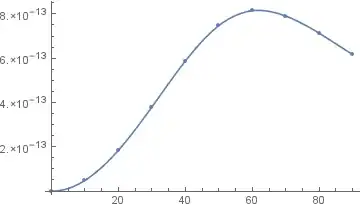
You can also use Interpolation[]

ip = Interpolation[data];
Show[ListPlot[data], Plot[ip[x], {x, 0, 90}]]

If you do use Interpolation, note that the derivative may not be what you want. You can choose the order of Interpolation by using InterpolationOrder->4 within the Interpolation[] function (4 is the default).

Plot[{nlm'[x], ip'[x]}, {x, 0, 90}]

Touché. OP didn't really give enough info about what he wanted though. — Feyre, Aug 10 '16 at 13:41
@Feye You're right, without direction from the OP, who knows which is the better approach. — Young, Aug 10 '16 at 13:43

Best fit curve for a data file

1 Answers1