1

I have the equation

$$ x(\phi)=\frac{1}{2\sqrt2}\left(\frac{-2}{\phi}+\log\left(\frac{1+\phi}{1-\phi}\right)\right) $$ I need to find the dependence $\phi(x)$, so I use NSolve:

B = 20;
NSteps = 2*B*100; 
H = N[2*B/NSteps];
X = Range[-B, B, H];
F[i_] := NSolve[x[ϕ] == i && (-1.0 <= ϕ <= 0.0), ϕ];
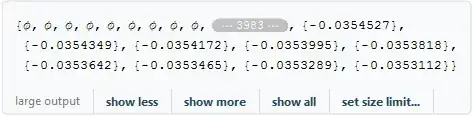
Monitor[PhiTable = Table[ϕ /. F[i], {i, -B, B, H}], i]

And I get this output:

Output

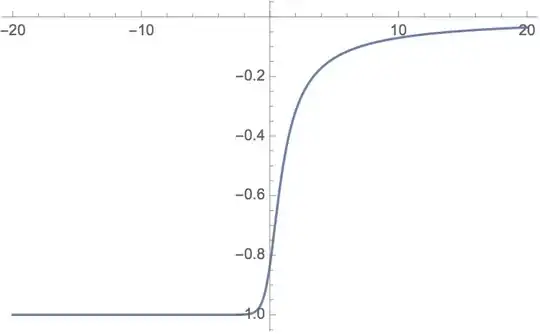
NSolve can't find the solution and it gives an empty result at the values from about -15 and lower. I suppose this bug is caused by exponential asymptotic of the function $\phi(x)$.

But when I write 

F[i_] := NSolve[x[ϕ] == i, ϕ, Reals];
Monitor[PhiTable = Table[ϕ /. F[i][[1]], {i, -B, B, H}], i]

It finds roots at the begining but freezes at the point 16.44 and higher.

Is there a way to fix it? Or shall I use another function, not NSolve?

Added:

x[ϕ_] := 1/(2 Sqrt[2]) (-2/ϕ + Log[(1 + ϕ)/(1 - ϕ)]);
Michael E2
  • 235,386
  • 17
  • 334
  • 747
Chertan
  • 13
  • 4
  • Welcome! I suggest the following:
    1. As you receive help, try to give it too, by answering questions in your area of expertise.
    2. Take the tour and check the faqs!
    3. When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign!
     –  Aug 11 '16 at 18:35
  • 1
    Could you give Mathematica code for your definition of x[\[Phi]]? Could be similar to this question. – Chris K Aug 11 '16 at 18:55
  • It looks like your equation $x(\phi) = x_0$ has two solutions for all values of $x_0$, one with positive $\phi$ and one with negative $\phi$. Do you have a preference as to which one is returned? – Michael Seifert Aug 11 '16 at 19:03
  • @ChrisK definition: x[[Phi]_] := 1/(2 Sqrt[2]) (-2/[Phi] + Log[(1 + [Phi])/(1 - [Phi])]); I also added it to the post as screenshot – Chertan Aug 11 '16 at 19:04
  • @MichaelSeifert yes, I need negative one. Therefore I used the restrictions on phi in the first example – Chertan Aug 11 '16 at 19:07
  • Sorry, I can't add the screenshot of the function x[[Phi]] due to my reputation. But it has the same view as the equation at the begining of the question. – Chertan Aug 11 '16 at 19:16
  • A side issue, unrelated to the problem: You should avoid starting your symbol names with a capital letter, especially single character variables. Quite a few are reserved symbols used by Mathematica. – Michael E2 Aug 11 '16 at 19:50

1 Answers1

1

The root tracker TrackRoot I wrote here can be applied to this problem. First, run TrackRoot from that link.

enter image description here

Then:

x[ϕ_] := 1/(2 Sqrt[2]) (-2/ϕ + Log[(1 + ϕ)/(1 - ϕ)]);
tr = TrackRoot[{x[ϕ] - xval}, {ϕ}, {xval, -20, 20}, 0, {-0.5}];
Plot[ϕ[x] /. tr, {x, -20, 20}]

enter image description here

Community
  • 1
Chris K
  • 20,207
  • 3
  • 39
  • 74
  • Thanks a lot, it works! Is it possible to correct this function and not to use interpolation? I'd like to get only values of phi. Sorry if it is a very foolish and simple question, I have never worked with manual functions before. – Chertan Aug 12 '16 at 14:22
  • @Chertan I'm not sure if this is exactly what you mean by correcting this function, but you can extract particular values of \[Phi] like this: \[Phi][1] /. tr gives -0.506903. – Chris K Aug 13 '16 at 01:39
  • yes, that's exactly what I meant. Thank you! – Chertan Aug 13 '16 at 13:42