4

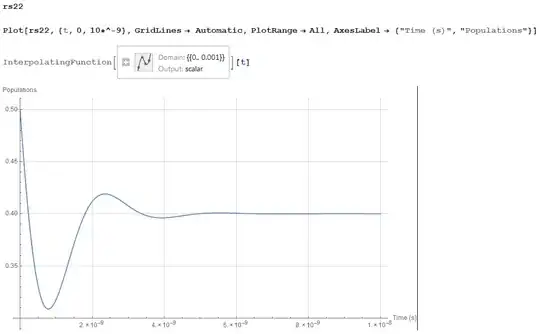
I have an interpolating function called rs22 - a solution from NDSolve - which is defined from 0 to about 1 ms. rs22 is a function that reaches a non-zero equilibrium value. (only shown here up to 10ns)

NDSolve Solution of rs22

I would like to perform a Fourier transform on this function. I have written down a line of code to do this but it doesn't work at the moment.

Needs["FourierSeries`"](*Yup I have this in my code, thanks for reminding ;)*)

Plot[NFourierTransform[rs22, t, dw, 
  Method -> {"GlobalAdaptive", Method -> "LevinRule", 
    "SymbolicProcessing" -> 0}], {dw, -1*^9, 1*^9}, PlotRange -> All,
  GridLines -> Automatic]

By definition a Fourier transform integrates from -inf to +inf. Is my interpolating function the problem since it is only defined up to 1ms?

I have also tried using NIntegrate instead but the solution changes with the total integration time which is something I don't want. But then again it seems sensible given the form of the product of the interpolating function and the exponential term: Exp(..)*rs22

xmin = -5*^9; xmax = 5*^9;
dwvec = DeleteCases[Table[dw, {dw, xmin, xmax, (xmax - xmin)/80}]];

output = ParallelTable[
   {Δω = dwvec[[j]]
    , popint = 
     NIntegrate[
      Exp[I Δω t] rs[2, 2], {t, 0, 1*^-3}
      , Method -> {"GlobalAdaptive", Method -> "LevinRule", 
        "SymbolicProcessing" -> 0}]}
   , {j, 1, Length[dwvec]}];

I am at loss as to how to perform this calculation.

Shiki
  • 73
  • 4
  • 6
    People here generally like users to post code as Mathematica code instead of images or TeX, so they can copy-paste it. It makes it convenient for them and more likely you will get someone to help you. You may find this this meta Q&A helpful – Michael E2 Aug 12 '16 at 16:43
  • 1
    You could try adding to your NDSolve[] code the option "ExtrapolationHandler" -> {0 &,"WarningMessage" -> False} – Michael E2 Aug 12 '16 at 18:35
  • 1
    Sorry I was in a bit of a hurry last week. I have edited the post. I added the line of code to NDSolve but it is giving me an error: "Unknown option !("ExtrapolationHandl‌​er") in Options[NDSolve]"

    I tried doing what is posted in here as well but it didn't work.

     – Shiki Aug 15 '16 at 13:15
  • 1
    (1) What version of Mathematica are you using? (2) Instead of the extrapolation handler, you could use Piecewise, something like the Fourier transform of Piecewise[{{r2ss, 0 < t < 10^-9}}, 0], or whatever domain instead of 0 < t < 10^-9 is appropriate. (3) Also, at some point, code for generating rs22 might be needed (it could be a fake one that generates the same kind of problem). – Michael E2 Aug 15 '16 at 13:43
  • 2
    (1) I'm using Mathematica 10.3 (2)With the Piecewise function the Fourier transform works. (3) I have prepared some code, not quite the exact problem. Now I am checking if the solution make sense since piecewise effectively truncates the solution beyond the range to 0 instead of having nothing like before. Definitely better than before though. Thanks! – Shiki Aug 15 '16 at 17:33

1 Answers1

4

From one of my comments:

You could use Piecewise, something like the Fourier transform of Piecewise[{{r2ss, 0 < t < 10^-9}}, 0], or whatever domain instead of 0 < t < 10^-9 is appropriate.

That is, something like:

NFourierTransform[Piecewise[{{r2ss, 0 < t < 10^-9}}, 0], t, dw, 
  Method -> {"GlobalAdaptive", Method -> "LevinRule", 
    "SymbolicProcessing" -> 0}]
Michael E2
  • 235,386
  • 17
  • 334
  • 747