I have two functions
f1[x_, y_] := -1 + x - Sqrt[8 + x^2 + (1 - x) (1 + x)];
f2[x_, y_] := -1 - x - Sqrt[8 y^2 + (1 - 3 x) (1 - x) + x^2];
I am searching the restriction and the relation between x and y in which f1 > f2. Also other condition in which f1<f2. But unfortunately I don't know what function must be used.

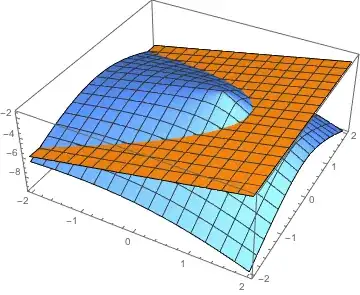

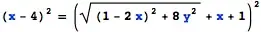
ContourPlot[f1[x, y] == f2[x, y], {x, -2, 2}, {y, -2, 2}]andPlot3D[{f1[x, y], f2[x, y]}, {x, -2, 2}, {y, -2, 2}]– chris Aug 19 '16 at 07:34f1 > f2andf1 < f2" is impossible. – m_goldberg Aug 19 '16 at 07:36