Two alternatives:
- Remove the argument restriction so that
ff[t] evaluates to Piecewise[..], which allows the discontinuity processing phase to see Piecewise and set up the integration scheme properly.
- Use
DiscreteVariables to code the function f.
Codes (OP's answer, Piecewise, DiscreteVariables):
Clear[f, fTmp];
fTmp[t_ /; 0 <= t <= 2] := \[Piecewise]{{1, t <= 1}, {0, t <= 2}};
f[t_] := fTmp[Mod[t, 2]];
{sol} = NDSolve[{a'[t] == f[t]*a[t], a[0] == 1}, a, {t, 0, 5},
Method -> {"DiscontinuityProcessing" -> False}];
Clear[ff, ffTmp];
ffTmp[t_ (*/;0 <= t <= 2*)] := \[Piecewise]{{1, t <= 1}, {0, t <= 2}};
ff[t_] := ffTmp[Mod[t, 2]];
{sol2} = NDSolve[{a'[t] == ff[t]*a[t], a[0] == 1}, a, {t, 0, 5}];
{sol3} = NDSolve[{a'[t] == fff[t]*a[t], a[0] == 1,
fff[0] == 1, WhenEvent[Mod[t, 1] == 0, fff[t] -> 1 - fff[t]]},
a, {t, 0, 5}, DiscreteVariables -> {fff}];
Comparison (time vs. steps and size of solution): The first alternative is better than the OP's, and the last is better than the first.
ListPlot[Flatten[a["Grid"] /. sol], GridLines -> {None, Automatic},
PlotLabel -> Row[{ByteCount@sol, "bytes"}, " "],
AxesLabel -> {"steps", "time"}
]

ListPlot[Flatten[a["Grid"] /. sol2], GridLines -> {None, Automatic},
PlotLabel -> Row[{ByteCount@sol2, "bytes"}, " "],
AxesLabel -> {"steps", "time"}
]
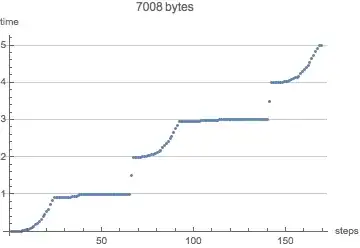
ListPlot[Flatten[a["Grid"] /. sol3], GridLines -> {None, Automatic},
PlotLabel -> Row[{ByteCount@sol3, "bytes"}, " "],
AxesLabel -> {"steps", "time"}
]

Another way for the given example is to use DSolve with the first alternative:
{sol4} = DSolve[{a'[t] == ff[t]*a[t], a[0] == 1}, a, {t, 0, 5}]

They produce overlapping plots:
Plot[a[t] /. {sol, sol2, sol3, sol4} // Evaluate, {t, 0, 5}]






