Plot point symbols at equispaced distance on a graph

Question

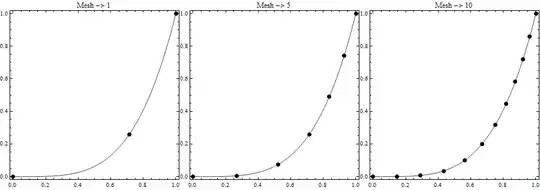
How to make the points on a graph equispaced?

x = Table[{ξ, ξ^4}, {ξ, 0, 1, 0.01}];
Δx = Differences[x];
Δl = Norm[#] & /@ Δx[[ ;; ]];
s = Flatten@{0, Accumulate[Δl]};
l = s[[-1]];
xint = {Interpolation[{s, x\[Transpose][[1]]}\[Transpose]], 
   Interpolation[{s, x\[Transpose][[2]]}\[Transpose]]};
Show[
 ListLinePlot[x],
 ListPlot[{xint[[1]][#], xint[[2]][#]} & /@ 
   Table[ξ, {ξ, 0, l, l/10}]],
 AspectRatio -> 1/GoldenRatio, Frame -> True, PlotRangePadding -> 0
 ]

With the above code I'm considering just equispaced points in the "geometric" space, but in the graph they are not, since I should include the contribution of the axis and the aspect ratio in the sampling.

Does anyone faced this problem before?

its not really clear what you want, but I think essentially you simply need to change Norm[#] to whatever distance metric you need, ( Norm[# {GoldenRatio,1}] perhaps ) — george2079, Aug 24 '16 at 19:38

score 2 · Answer 1 · answered Aug 25 '16 at 00:02

A copy of your code:

x = Table[{ξ, ξ^4}, {ξ, 0, 1, 0.01}];
Δx = Differences[x];
Δl = Norm[#] & /@ Δx[[ ;; ]];
s = Flatten@{0, Accumulate[Δl]};
l = s[[-1]];
xint = {Interpolation[{s, x\[Transpose][[1]]}\[Transpose]], 
   Interpolation[{s, x\[Transpose][[2]]}\[Transpose]]};

If we make a table of the XY pairs

tableXY = {xint[[1]][#], xint[[2]][#]} & /@ Table[ξ, {ξ, 0, l, l/10}]

(* {{0., 0.}, {0.160018, 0.000655661}, {0.319654, 0.0104405},
   {0.474059, 0.0505046}, {0.608027, 0.136676}, {0.712369, 0.257525},
  {0.793057, 0.395566}, {0.857941, 0.541788}, {0.912171, 0.692317},
  {0.958872, 0.845361}, {1., 1.}} *)]

Take the difference and apply Norm

tableXYD = Differences@tableXY;

Norm[#] & /@ tableXYD

(* {0.16002, 0.159936, 0.159518, 0.159288, 0.159662, 0.159893, \
0.159972, 0.159999, 0.16001, 0.160015} *)

shows that you have succeeded in getting the distances approximately equal.

In order to plot it with equal distance set the AspectRatio to 1.

Show[
 ListLinePlot[x],
 ListPlot[
  {xint[[1]][#], xint[[2]][#]} & /@ Table[\[Xi], {\[Xi], 0, l, l/10}],
  PlotStyle -> {Black, PointSize[0.03]}
  ],
 AspectRatio -> 1,
 Frame -> True,
 PlotRangePadding -> 0.02
 ]

Mathematica graphics

If you want an aspect ratio other than one and want the graph to appear to have equal distance you will have to develop an algorithm to compensate for the aspect ratio (should not be too difficult).

as suggest by george2079 a straightforward though partial solution is given by adding a scale to the Norm[], that is Norm[# {1, 1/GoldenRatio}] & /@ [CapitalDelta]x[[ ;; ]];. However this is valid when the graph has 1:1 axis, as in the solution you have proposed. below I post a more "general" solution. — Fabio, Aug 25 '16 at 07:02

score 2 · Answer 2 · answered Jul 04 '17 at 00:02

You can also use MeshFunctions->{"ArcLength"}

ListLinePlot[x, MeshFunctions -> {"ArcLength"}, Mesh -> #, MeshStyle -> PointSize[Large], 
 AspectRatio -> 1, Frame -> True, ImageSize -> 300, PlotLabel -> Row[{"Mesh -> " , #}]] /. 
 ll_Line :> {ll, PointSize[Large], Black, Point[ll[[1, {1, -1}]]]} & /@ {1, 5, 10} // Row

Mathematica graphics

score 0 · Answer 3 · edited Aug 25 '16 at 07:22

This should be ok also when the axis are not 1:1 in scale (not the aspect ratio but the axis scale, I mean)

xmax = 2;
ymax = 3;
ar = 1/3;
np = 10;
x = Table[{ξ, ymax (ξ/xmax)^4}, {ξ, 0, xmax, 0.01}];
Δx = Differences[x];
Δl = 
  Norm[# {1/xmax, ar/ymax}] & /@ Δx[[ ;; ]];
s = Flatten@{0, Accumulate[Δl]};
l = s[[-1]];
xint = {Interpolation[{s, x\[Transpose][[1]]}\[Transpose]], 
   Interpolation[{s, x\[Transpose][[2]]}\[Transpose]]};
Show[
 ListLinePlot[x],
 ListPlot[{xint[[1]][#], xint[[2]][#]} & /@ 
   Table[ξ, {ξ, 0, l, l/np}], 
  PlotMarkers -> {Graphics[Disk[]], 0.08}],
 AspectRatio -> ar, Frame -> True, PlotRangePadding -> 0
 ]

Plot point symbols at equispaced distance on a graph

3 Answers3

Linked