3

When I make the plot

Plot[-x^2 E^-x^2, {x, -10, 10}, PlotRange -> All]

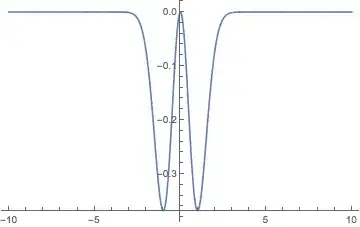
Mathematica graphics

it results in two peaks around {-1, -.34}, {+1, -.34}

But when I specify a vastly expanded plot domain

Plot[-x^2 E^-x^2, {x, -1000, 1000}, PlotRange -> All]

Mathematica graphics

the result looks completely different.

Why does this happen and how do I handle this situation?

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Aroldo Ribeiro
  • 33
  • 6
  • 1
    Have a look at PlotPoints – Feyre Aug 31 '16 at 15:03
  • 1
    Setting PlotPoints->200 does fix the problem, but I do think Plot should be a bit better at sampling functions like this. – Jason B. Aug 31 '16 at 15:04
  • 5
    Sampling granularity is going to be an issue, especially in large domains where the "action" is heavily localized. – Daniel Lichtblau Aug 31 '16 at 15:12
  • Thank for a good "warning" question! – atapaka Aug 31 '16 at 15:19
  • 1
    @JasonB OK, but how would Plot achieve that? What it already does it pretty advanced, I think. What method would you propose to let it discover the interesting region when it is tiny, without making it too slow? It seems to me that its behaviour is quite reasonable here. – Szabolcs Aug 31 '16 at 16:31
  • @Szabolcs - (bad joke removed) You are correct, I was speaking of things I'm not an expert in. Will leave comment for the continuity of the discussion, but your point is taken. – Jason B. Aug 31 '16 at 17:17
  • It is interesting to use EvaluationMonitor on this. After the initial sampling of 50 evenly spaced points on {-1000,1000} it samples 27 more points, every one within 2% of the ends. (??) Why on earth would it not resample near the largest spike in the data? – george2079 Aug 31 '16 at 17:30
  • @JasonB I'm not just trying to make a point. If you have any idea at all about how this might be handled better than it already is, I am really interested. The algorithm Plot uses is simple enough that it can be reimplemented relatively quickly in Mathematica. It's a good problem to experiment with. – Szabolcs Aug 31 '16 at 17:44
  • 1
    Strongly related: "Strange Sin[x] graph in Mathematica." – Alexey Popkov Sep 01 '16 at 07:37
  • 1
    Related: "How does Plot work?" – Alexey Popkov Sep 01 '16 at 07:39

1 Answers1

3

Since the function is obviously even, you need only Plot one side. Given a wide PlotRange using LogLinearPlot helps to find and see the "action"

Minimize[{-x^2 E^-x^2, x > 0}, x, Reals]

(*  {-(1/E), {x -> 1}}  *)

LogLinearPlot[-x^2 E^-x^2, {x, .001, 1000}, PlotRange -> All,
 Epilog -> {Red, Dashed, Line[{{Log[1], 0}, {Log[1], -1/E}}]}]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198