How to get exact point of intersection of a plot with axis?

Question

I have a parametric plot y(t) vs. x(t). I want to know exactly at what value of x, this y vs x curve crosses the x-axis? I tried with "Get coordinates" of Drawing tools but this is not so accurate. Can anyone please tell me how I can print the exact point of intersection between this curve and x-axis?

I want to find at what value of t, dbdt becomes zero.

I had tried with Solve too. But it was taking so much time (more than half an hour and still running) to print output! Actually these functions are not so simple. They both are like implicit functions f(x(y(z...)))). I don't care about the value of the independent variable t at which y becomes zero. I need the value of x only. If there is a faster way, please let me know. — cosmos, Sep 05 '16 at 20:57
A = 1 + 2/Sqrt[x^2 + 1]; A0 = 1 + 2/Sqrt[x0^2 + 1]; B = 2* Re[ NIntegrate[ 1/(\[x]^2*A^2*Sqrt[1/(x0^2*A0^4) - 1/(x^2*A^4)]), {x, x0, \[Infinity]}]] t = ArcSin[x0*A0^2] (*dadr and dtdr are derivatives of B and t*) dbdt = (Cos[b]/ Cos[t] )^2*(1 - 1/2*(1 + ( Cos[t] /Cos[B - t])^2 (dBdr/ dtdr - 1))) (*where b is a function like ArcTan[some function of B,t]*) Now I want to know at what value of t dbdt becomes zero. — cosmos, Sep 05 '16 at 21:14
i can't write full code because it's part of my new project. — cosmos, Sep 05 '16 at 21:15
@BenKalziqi Yes, I tried with NSolve too. Same problem. Too much time taking. No output even after running for nearly half an hour. — cosmos, Sep 05 '16 at 21:17
Please edit your question with the code, and provide a functioning code, this code won't run. — Feyre, Sep 05 '16 at 21:17
Provide the values of x0 etc. What is the parametric variable? — corey979, Sep 05 '16 at 21:31
@Feyre I just added the code in my question. Please see if it helps in understanding my question. — cosmos, Sep 05 '16 at 21:31
x0 is the independent variable. I can choose any value between 0 to \infty. — cosmos, Sep 05 '16 at 21:32
FindRoot[] is the way to find roots numerically, especially of equations that are difficult (e.g. non-analytic, use a numerical procedure such as NIntegrate, etc.). You should post code that adequately reproduces the computational issue you're having, but it doesn't have to be your private/confidential code. — Michael E2, Sep 05 '16 at 21:46
The code as it stands is not functional - it does return only errors. Please provide a minimal working example. — corey979, Sep 05 '16 at 21:47
It still doesn't work. You're trying NIntegrate[] to a non-numerical value x0. — Feyre, Sep 06 '16 at 07:02
Please check the code. The range of x0 is {x0, 0.001, 50}. Obviously it is not non-numerical value. I don't understand why mathematica shows such errors and still plots A(x0). If x0 were indeed non-numerical, why is mathematica plotting A(x0)? — cosmos, Sep 06 '16 at 08:00

score 4 · Answer 1 · answered Sep 05 '16 at 21:24

4

You may use MeshFunctions, though I don't know the precision :

gr00 = ParametricPlot[{t, t^2 - 1}, {t, 0, 2}, Mesh -> {{0}}, 
  MeshFunctions ->  {#2 &}, 
  MeshStyle -> Directive[Black, PointSize[.05]]]

Cases[Normal[gr00], Point[___], {1, Infinity}]

{Point[{0.999811, 0.}]}

answered Sep 05 '16 at 21:24

andre314

18,474
1
36
69

I got blank {{}} as output! – cosmos Sep 05 '16 at 22:12
This probably won't work if the curve is tangent to the axis. Not sure what to recommend for that case. – Michael E2 Sep 07 '16 at 12:52

score 2 · Answer 2 · edited Apr 13 '17 at 12:55

Consider

x[u_] := Sin[u]
y[u_] := Sin[2 u]
ParametricPlot[{x[u], y[u]}, {u, 0, 2 Pi}]

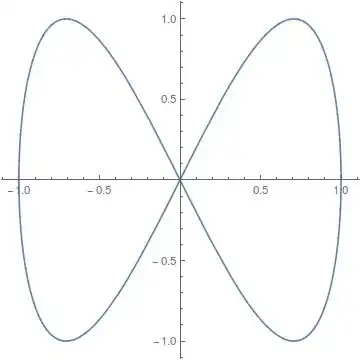
Solve for u an equation $y(u)=0$:

sol = u /. Solve[y[u] == 0, u]

{ConditionalExpression[[Pi] C1, C1 [Element] Integers], ConditionalExpression[1/2 ([Pi] + 2 [Pi] C1), C1 [Element] Integers]}

Evaluate x[u] taking sol as input and taking into account the conditions from the ConditionalExpressions:

Table[Simplify[x[sol[[i]]], Assumptions -> sol[[i, 2]]], {i, 1, Length@sol}]

{0, (-1)^C1}

One probably has to check what values can C[1] take (in this case Integers), so maybe instead

Simplify[x[sol], Assumptions -> sol]

{ConditionalExpression[Sin[[Pi] C1], C1 [Element] Integers], ConditionalExpression[Cos[[Pi] C1], C1 [Element] Integers]}

which on the other hand returns a slightly less clear solution.

EDIT: I developed a different method, suitable for this problem also, while answering another question.

Let's take the plot in the form

x[u_] := Sin[u]
y[u_] := Sin[2 u]
curve = Show[
  ParametricPlot[{x[u], y[u]}, {u, 0, 2 Pi}, Axes -> None, 
   PlotRangePadding -> None], 
  Plot[0, {x, -1, 1}, Axes -> None, PlotRangePadding -> None]]

and extract the pixel positions of intersection with

px = PixelValuePositions[#, White] & @
  MorphologicalBranchPoints @ Thinning @ Binarize @ ColorNegate @ curve

{{180, 182}, {2, 180}, {180, 180}, {359, 180}, {180, 179}}

We need to connect them to the actual coordinates on the plot:

pl = PlotRange@curve

{{-1., 1.}, {-1., 0.999999}}

id = ImageDimensions@curve

{360, 360}

The relation between pl and id is linear, $y=ax+b$ and $y=cx+d$ in the horizontal and vertical directions, respecively:

{a, b} = {a, b} /. 
  First@Solve[{pl[[1, 1]] == b, pl[[1, 2]] == a id[[1]] + b}, {a, b}]
{c, d} = {c, d} /. 
  First@Solve[{pl[[2, 1]] == d, pl[[2, 2]] == c id[[2]] + d}, {c, d}]

{0.00555555, -1.}

{0.00555555, -1.}

The pixel positions transformed to plot coordinates:

ic = {a #1 + b, c #2 + d} & @@@ px

{{9.49664*10^-9, 0.011111}, {-0.988889, -1.50139*10^-7}, {9.49664*10^-9, \ -1.50139*10^-7}, {0.994444, -1.50139*10^-7}, {9.49664*10^-9, \ -0.0055557}}

look like this:

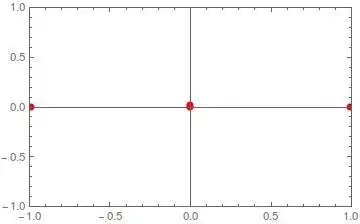
We can get rid of the ambiguity (5 points for 3 intersections) with clustering:

clu = ClusterClassify[ic, Method -> "DBSCAN"]

Number of clusters: 3

g = GatherBy[ic, clu]
icmean = Chop[#, 10^-6] &@Reverse[Mean /@ g]

{{0.994444, 0}, {-0.988889, 0}, {0, 0.0018517}}

Show[curve, Graphics[{PointSize[Large], Point[#]}] &@icmean]

which looks very good; icmean are the positions of the three intersections.

How to get exact point of intersection of a plot with axis?

2 Answers2