Simultaneous fitting of ParametricNDSolve with varying initial conditions

Question

Edit: Issue solved - code at end

I am fitting 3 enzyme kinetics data sets. They are all from the same enzyme, but with different initial conditions. I am unsure of how to simultaneously fit 3 different ParametricNDSolve containing different initial conditions simultaneously using NonlinearModelFit.

The data sets are:

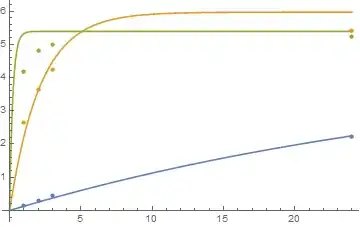
data0={{1, 0.14}, {2, 0.29}, {3, 0.45}, {24, 2.21}};
i0=4.5;
data200={{1, 2.65}, {2, 3.63}, {3, 4.25}, {24, 5.40}};
i200=5.97;
data2000={{1, 4.17}, {2, 4.80}, {3, 4.99}, {24, 5.24}};
i2000=5.39;

I'm fitting it to the following system of differential equations:

eS'[t]==-k1*eS[t]-k2*eS[t]*G[t],
G'[t]==-k2*eS[t]*G[t],
eG'[t]==k2*eS[t]*G[t],
e'[t]==k1*eS[t],
eT'[t]==k1*eS[t]+k2*eS[t]*G[t]

The data points correspond to eT[t]. In regards to the initial conditions, the following remain constant between the 3 data sets:

eG[0]==0,
e[0]==0,
eT[0]==0

However, two of the initial conditions change depending on the data set. For data0,

eS[0]==i0,
G[0]==0

For data200,

eS[0]==i200,
G[0]==200

For data2000,

eS[0]==i2000,
G[0]==2000

For any individual data set, I know how to find a fit for the parameters k1 and k2 as follows (for data200):

par200=ParametricNDSolve[{
eS'[t]==-k1*eS[t]-k2*eS[t]*G[t],
G'[t]==-k2*eS[t]*G[t],
eG'[t]==k2*eS[t]*G[t],
e'[t]==k1*eS[t],
eT'[t]==k1*eS[t]+k2*eS[t]*G[t],
eG[0]==0,
e[0]==0,
eT[0]==0,
eS[0]==i200,
G[0]==200},
{eG,e,eT,eS},{t,0,24},{k1,k2}];

fit=NonlinearModelFit[data200,{eT[k1,k2][t]/.par200,k1>0,k2>0},{k1,k2},t,Method->"NMinimize"];

I can obtain values for k1 and k2 for each data set individually, but I would like to fit for k1 and k2 from all 3 data sets simultaneously. I was thinking of merging all three data sets together and identifying them by a dummy variable as follows:

data=Join[
data0/.{t_,y_}->{1,t,y},
data200/.{t_,y_}->{2,t,y},
data2000/.{t_,y_}->{3,t,y}];

However, then I get stuck: I'm not sure how to setup the function in NonlinearModelFit such that only eT[k1,k2][t]/.par0 is used when the dummy variable is 1, only eT[k1,k2][t]/.par200 is used when the dummy variable is 2, etc...

I've seen the following answers in stackexchange: 1 and 2, but both are trying to fit data sets where either the initial conditions aren't changing or ParametricNDSolve isn't used. I've been unsuccessful at trying to adapt the answers for either to tackle my issue.

Thanks for any help.

Solution So basically, use of KroneckerDelta basically solves everything. Assuming that par0 is setup analogous to par200 above,

model0[index_,t_,k1_,k2_]=KroneckerDelta[index,1]*eT[k1,k2][t]/.par0;
model200[index_,t_,k1_,k2_]=KroneckerDelta[index,2]*eT[k1,k2][t]/.par200;
model[index_,t_,k1_,k2_]=model0[index, t, k1, k2]+model200[index, t, k1, k2];

fit=NonlinearModelfit[data,{model[index,t,k1,k2],k1>0,k2>0},{k1,k2},{index,t},Method->"NMinimize"];

This will fit the data0 and data200 data sets simultaneously. If you want to fit all 3 data sets, include the corresponding code for par2000 and model2000.

Answer 1

A solution can be obtained, roughly following the approach in question 84063. Recast the data and, for convenience, the initial conditions as,

data = Join[Join[{1}, #] & /@ data0, Join[{2}, #] & /@ data200, 
    Join[{3}, #] & /@ data2000];
init = {{i0, 0}, {i200, 200} , {i2000, 2000}};

Then, solutions to the ODEs are given by

par = (ParametricNDSolveValue[{eS'[t] == -k1*eS[t] - k2*eS[t]*G[t], 
    G'[t] == -k2*eS[t]*G[t], eG'[t] == k2*eS[t]*G[t], 
    e'[t] == k1*eS[t], eT'[t] == k1*eS[t] + k2*eS[t]*G[t], 
    eG[0] == 0, e[0] == 0, eT[0] == 0, eS[0] == First@#, G[0] == Last@#}, 
    eT, {t, 0, 24}, {k1, k2}] & /@ init) // Flatten;

(only eT needs to be stored), the model by

model[k1_, k2_][i_, t_] := par[[i]][k1, k2][t] /; And @@ NumericQ /@ {k1, k2, i, t}];

and finally the fitted solution by

fit = NonlinearModelFit[data, model[k1, k2][i, t], {{k1, .03}, {k2, .002}}, {i, t}];
fit["ParameterTable"]

Show[Plot[{fit[1, t], fit[2, t], fit[3, t]}, {t, 0, 24}], 
    ListPlot[{data0, data200, data2000}]]

More data points presumably would yield a better fit, although the one obtained is not bad.