Symbolic determinant is not computing

Question

I'm trying to compute the determinant of a symbolic matrix made with the following code:

NewMatrix[n_] := Module[{i = 1, j = 1, M = Array[m, {n + 1, n + 1}]},
  For[i = 1, i <= n + 1, i++,
   For[j = 1, j <= n + 1, j++,
    If[j < i, m[i, j] = a[[j]],
     If[j == i, m[i, j] = x,
      If[j > i, m[i, j] = a[[j - 1]], 0]]]
    ]
   ]; M // MatrixForm]

But when I apply:

Det[NewMatrix[4]]

Mathematica returns this:

If I try to give a and x numerical values it still doesn't show the numerical value of the determinant, just gives the same expression but with numbers. What is happening here?

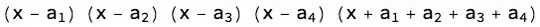
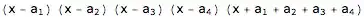
Your output, NewMatrix[4], is in the MatrixForm, while Det can be applied to Lists; first, remove the //MatrixForm part and it will work. However, I'm getting an error: Part::partd: "Part specification a[[1]] is longer than depth of object." — corey979, Sep 11 '16 at 16:11
Regarding the error: insert also a = Array[a, n] into the Module, after i and j, and before M. — corey979, Sep 11 '16 at 16:19

Bob Hanlon · Accepted Answer · 2016-09-11T16:55:11.913

Do not include MatrixForm in the definition of NewMatrix; wrappers are only used for display. Also use an indexed variable rather than using Part for a.

Format[a[n_]] := Subscript[a, n]

NewMatrix[n_Integer?Positive] :=
 Module[
  {i = 1, j = 1, M = Array[m, {n + 1, n + 1}]},
  For[i = 1, i <= n + 1, i++,
   For[j = 1, j <= n + 1, j++,
    If[j < i, m[i, j] = a[j],
     If[j == i, m[i, j] = x,
      If[j > i, m[i, j] = a[j - 1], 0]]]]]; M]

NewMatrix[4] // MatrixForm

Det[NewMatrix[4]]

% // Simplify

detNewMatrix[n_Integer?Positive] :=
 Module[
  {arr = Array[a, n]},
  (x + Total[arr])*(Times @@ (x - arr))]

Verifying that this is the determinant

And @@ Table[detNewMatrix[n] == Det[NewMatrix[n]] // 
  Simplify, {n, 10}]

(*  True  *)

score 2 · Answer 2 · edited Apr 13 '17 at 12:56

I'm assuming that a is (going to be) a vector, since you index it with Part. In that case, here is a simpler way:

newMatrix[n_Integer?Positive] := 
  With[{v = Array[Indexed[a, #] &, n]},
   Table[Insert[v, x, i], {i, n + 1}]];

mat = newMatrix[4];
mat // MatrixForm

Mathematica graphics

Det[mat] // Simplify

Mathematica graphics

You can inject a vector for a using ReplaceAll:

mat /. a -> {1, 12, 23, 34}
% // MatrixForm
(*
  {{x, 1, 12, 23, 34},
   {1, x, 12, 23, 34},
   {1, 12, x, 23, 34},
   {1, 12, 23, x, 34},
   {1, 12, 23, 34, x}}
*)

Mathematica graphics

See Why does MatrixForm affect calculations? for answers to why MatrixForm messes up the computation.

For more alternatives to For loops, see this answer or search the site.

Symbolic determinant is not computing

2 Answers2

Linked