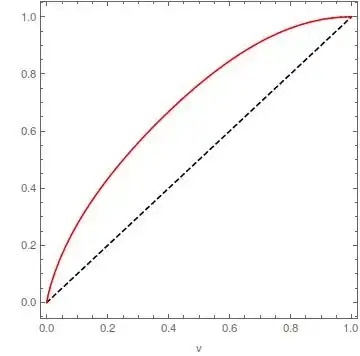
Assuming $0<x,y<1$ and $0<v<1$, consider the function $f(x,y)=1+(1-2x)(1-2y)$. How to find the integral $I=\int_{\{xy+xy(1-x)(1-y)\leq v\}} \,f(x,y)\;dx \, dy$ using Mathematica or Matlab?
I am trying to show that $I \leq v$ by this integral for which the integration of $f(x,y)$ over the region $\{ xy+xy(1-x)(1-y) \leq v\}$ is essential.