How could I perform Region or Polygon Clipping in mathematica?

Question

I need to clip several regions reg: like Rectangle, Polygon, Ellipse... My goal isn't to plot the clipping but to have a representation of each new region.

I searched if there was any package or function to perform polygon clipping at least, but I couldn't find any lead.

My main question is:

Is there an already implemented algorithm in mathematica to perform polygon or region clipping ?

else:

Should I better link an external polygon clipping library (such as Clipper, Boost.Geometry or CGAL) with mathematica to do so ?

Edit:

To illustrate what I aim for:

I have 5 rectangles that are overlapping, I would like to have:

I have now 8 regions that aren't intersecting/overlapping with others.

I have edit my question to illustrate my problem. @Szabolcs It must in fact use RegionIntersection, but also RegionDifference... I tried a custom solution to do such result, but it's not working that well on any kind of polygons or regions disposition. — A.M., Sep 16 '16 at 11:16
Related: "How do I flatten transparency on a graphics, for conversion to eps or similar?" — Alexey Popkov, Sep 17 '16 at 08:35

george2079 · Answer 1 · 2016-09-16T18:47:08.630

7

Using boolean operations to test every possible combination of area intersections:

r1 = Disk[{0, 0}, 1];
r2 = Disk[{1/8, 0}, {1/2, 3/2}];
r3 = Rectangle[{1/4, 0}, {2, 1}];
regions={r1,r2,r3};
Graphics[{Opacity[.5], {{Red, r1}, {Green, r2}, {Blue, r3}}}]

range = {{-2,2},{-2,2}};
(*warning RegionPlot throws errors
    if nothing is in the plot range*)
sub[set_, r_] := 
 Module[{
   in = Flatten@Position[set, 1], 
   out = Flatten@Position[set, 0]}, 
  If[Union@set === {1}, RegionIntersection @@ r, 
   RegionDifference[
      BooleanRegion[And, r[[in]]], 
      BooleanRegion[Or, r[[out]]]]]]
c = Tuples[{0, 1}, Length@regions][[2 ;;]]; (*dont include first tuple {0,0,..}*)
subregions = Select[sub[#, regions] & /@ c, Area@# > 0 &];
s = MapThread[RegionPlot[#1, PlotStyle -> #2, PlotRange -> range] &,
   {subregions, 
    Table[Hue[RandomReal[{0, 2/3}]], {Length@subregions}]}];
Grid[{s, c}]
Show[s, PlotRange -> range]

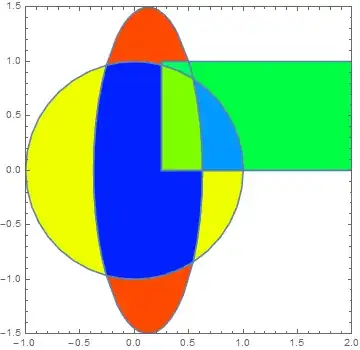
notice there are disconnected sub regions that happen when a single region is split by the others. Kind of stumped on how to split those automatically into separate regions.

edit per comment from @JasonB we can get all the discrete regions, but it requires generating mesh regions:

  ConnectedMeshComponents@DiscretizeRegion[#] & /@ subregions

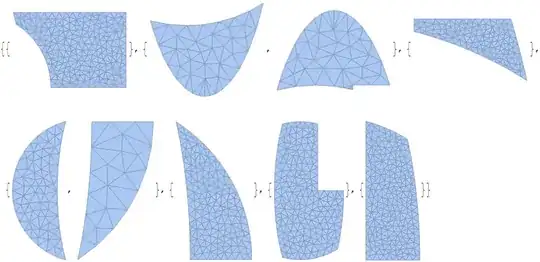
edit: the example

regions = {Rectangle[{5, -15}, {35, 15}], 
   Rectangle[{25, -20}, {45, 20}], Rectangle[{20, -5}, {35, 5}], 
   Rectangle[{30, 10}, {45, 20}], Rectangle[{35, -20}, {45, -5}]};
range = {{0, 50}, {-30, 30}}

edited Sep 16 '16 at 18:47

answered Sep 16 '16 at 13:55

george2079

38,913
1
43
110

Thanks for your reply @george2079 However, c variable definition is missing, what is the set_ arguments for ? – A.M. Sep 16 '16 at 14:30
sort for the excessive editing... now its working right..! excepting for the pesky issue of how to split the disconnected regions. – george2079 Sep 16 '16 at 15:33
@george2079 - you can use ConnectedMeshComponents – Jason B. Sep 16 '16 at 15:53
@JasonB, thanks - added that. – george2079 Sep 16 '16 at 16:03
@george2079 I've tried your code on my example regions = {Rectangle[{5, -15}, {35, 15}], Rectangle[{25, -20}, {45, 20}], Rectangle[{20, -5}, {35, 5}], Rectangle[{30, 10}, {45, 20}], Rectangle[{35, -20}, {45, -5}]} and I have issues with RegionPlot::nnregion and RegionPlot::nnregion – A.M. Sep 16 '16 at 17:53
making me work!.. Two fixes needed: use Area to eliminate empty regions. Also the PlotRange was hard coded. – george2079 Sep 16 '16 at 18:32
Thanks a lot @george2079, working pretty well now ! – A.M. Sep 19 '16 at 07:59

How could I perform Region or Polygon Clipping in mathematica?

1 Answers1

Linked