Missing error bars

Question

In preparing an example to answer this question How to plot data as (X,Y) points with error bars on Y, I came across a case with missing error bars. (In my answer, I got round the problem by using approximate rather than exact numbers).

The following data

x = Sqrt[Range[10]];
y = Sin[x];
e = 1/x;

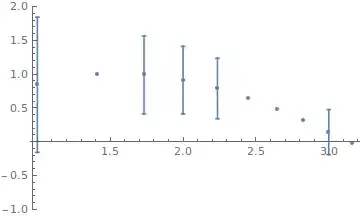
Creates an error bar plot with some bars missing

Needs["ErrorBarPlots`"]
list1 = MapThread[{{#1, #2}, ErrorBar[#3]} &, {x, y, e}]
ErrorListPlot[list1, PlotRange -> {-1, 2}]
(* {{{1, Sin[1]}, ErrorBar[1]}, {{Sqrt[2], Sin[Sqrt[2]]}, 
  ErrorBar[1/Sqrt[2]]}, {{Sqrt[3], Sin[Sqrt[3]]}, 
  ErrorBar[1/Sqrt[3]]}, {{2, Sin[2]}, 
  ErrorBar[1/2]}, {{Sqrt[5], Sin[Sqrt[5]]}, 
  ErrorBar[1/Sqrt[5]]}, {{Sqrt[6], Sin[Sqrt[6]]}, 
  ErrorBar[1/Sqrt[6]]}, {{Sqrt[7], Sin[Sqrt[7]]}, 
  ErrorBar[1/Sqrt[7]]}, {{2 Sqrt[2], Sin[2 Sqrt[2]]}, 
  ErrorBar[1/(2 Sqrt[2])]}, {{3, Sin[3]}, 
  ErrorBar[1/3]}, {{Sqrt[10], Sin[Sqrt[10]]}, ErrorBar[1/Sqrt[10]]}} *)

However, a very similar example (the same size error bars) doesn't have this problem

Needs["ErrorBarPlots`"]
list2 = MapThread[{{#1, #2}, ErrorBar[#3]} &, {x, x, e}]
ErrorListPlot[list2, PlotRange -> {-1, 4}]
(* {{{1, 1}, ErrorBar[1]}, {{Sqrt[2], Sqrt[2]}, 
  ErrorBar[1/Sqrt[2]]}, {{Sqrt[3], Sqrt[3]}, 
  ErrorBar[1/Sqrt[3]]}, {{2, 2}, ErrorBar[1/2]}, {{Sqrt[5], Sqrt[5]}, 
  ErrorBar[1/Sqrt[5]]}, {{Sqrt[6], Sqrt[6]}, 
  ErrorBar[1/Sqrt[6]]}, {{Sqrt[7], Sqrt[7]}, 
  ErrorBar[1/Sqrt[7]]}, {{2 Sqrt[2], 2 Sqrt[2]}, 
  ErrorBar[1/(2 Sqrt[2])]}, {{3, 3}, 
  ErrorBar[1/3]}, {{Sqrt[10], Sqrt[10]}, ErrorBar[1/Sqrt[10]]}} *)

Is this a bug?