This is a new question which I will reuse the codes of a previous question (When to use GeometricTransformation or Rotate) that belongs to me.
I am doing this way because these questions have different goals and I am progressing this way.
With the help of the user Sjoerd C. de Vries I learned how to rotate an object graph that I am calling of cam.
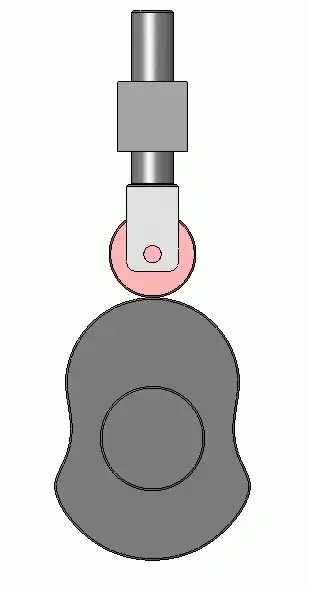
Now I came across another problem. How to make my valve stays tangent in the whole course of the cam?
Here is a link to what I'm trying to show: CamShaft
My code:
r1 = 15; r2 = 8; c = 50; γ = ArcSin[(r1 - r2)/c] // N;
l1 = (2 γ + π) r1;
l2 = (π - 2 γ) r2;
l3 = 2 c Cos[γ];
L = 2 c Cos[γ] + (2 γ + π) r1 + (π -
2 γ) r2;
cam = {Circle[{0, 0}, r1, {Pi/2 - γ, ((3*Pi))/2 + γ}],
Circle[{c, 0}, r2, {Pi/2 - γ, -(Pi/2) + γ}],
Line[{{Cos[Pi/2 - γ]*r1,
Sin[Pi/2 - γ]*r1}, {Cos[Pi/2 - γ]*r2 + c,
Sin[Pi/2 - γ]*r2}}],
Line[{{Cos[((3*Pi))/2 + γ]*r1,
Sin[((3*Pi))/2 + γ]*r1}, {Cos[-(Pi/2) + γ]*r2 + c,
Sin[-(Pi/2) + γ]*r2}}], PointSize[0.03], Point[{0, 0}]};
g = Graphics[cam];
valve = Graphics[
{
Red,
Thickness[0.008],
Circle[{0, posição = 15 + rValve}, rValve = 4, {0, -Pi}],
Line[{{-rValve, posição}, {-rValve, posição + 20}}],
Line[{{rValve, posição}, {rValve, posição + 20}}],
Line[{{-rValve, posição + 20}, {rValve, posição + 20}}]
}
];
Show[g, valve]
The code is represented an initial position of my study because I cannot develop the next steps.
I do not know how to make the valve tap the cam throughout the course.


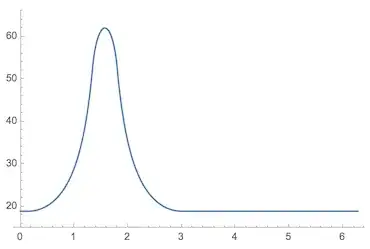

PerformanceGoal -> "Speed". That gave me about a 4 times speedup. – Greg Hurst Sep 22 '16 at 20:20PlotandPolarPlot. – Greg Hurst Sep 22 '16 at 20:30