ListPlot3D accepts RegionFunction, so let's exploit this fact. The idea is to create a region.
data = Flatten[#, 1] &@
Table[{x, y, 1}, {x, 0, 5, 5/60}, {y, Sin[x],
Cos[x] + 3, (Cos[x] + 3 - Sin[x])/60}]
data2D = data[[All, 1 ;; 2]]
range = {{0, 5}, {-1, 4}}
First, Binarize the region
reg = Binarize@
ListPlot[data2D, Axes -> False, AspectRatio -> 1,
PlotStyle -> PointSize -> Large]
so that one can use the functions of bobthechemist and rhermans:
binaryImageToRegion[bimg_] :=
With[{idata = ImageData[bimg], xmax = First@ImageDimensions[bimg],
ymax = Last@ImageDimensions[bimg]},
BoundaryDiscretizeGraphics@
First@RegionPlot[
idata[[IntegerPart@(ymax - y), IntegerPart@x]] == 1, {x, 1,
xmax}, {y, 1, ymax}]]
reg1 = binaryImageToRegion[ColorNegate@reg]

{100, 100} \[Element] reg1
{200, 200} \[Element] reg1
False
True
and
imgregion[im_] :=
Polygon[Part[#, Last@FindShortestTour[#]] &@
PixelValuePositions[
MorphologicalPerimeter[
Erosion[FillingTransform@ColorNegate@Binarize[im, 0.91], 2],
CornerNeighbors -> False], 1]]
reg2 = BoundaryDiscretizeRegion@imgregion[reg];
plot = RegionPlot@reg2

{100, 100} \[Element] reg2
{200, 200} \[Element] reg2
False
True
I'll use reg1 here; exactly the same results were obtained with reg2.
We need to translate the coordinates in data, which are in the range, so that they correspond to those in reg1. We need to take dimensions of the RegionPlot of reg1, without the Frame:
id = ImageDimensions @ RegionPlot[#, Frame -> None] &@reg1
{360, 360}
I calculated it with pen and paper, but it's easy (the transformation is linear) to do it automatically. With the derived RegionFunction:
ListPlot3D[data,
RegionFunction ->
Function[{x, y, z}, {72 x, (y + 1) 72} \[Element] reg1]]



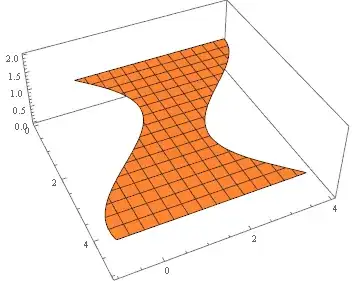





RegionPlot3D[ Sin[x] < y < Cos[x] + 3 && z == 1, {x, 0, 5}, {y, -1, 4}, {z, 0, 2}]? – N.J.Evans Sep 27 '16 at 20:18